Полезная информация о статических упражнениях FITNESS 24
Несомненно, мужчины, посещающие фитнес-клуб, хотят иметь тело атлета, поэтому часто тягают по-настоящему тяжелые снаряды и достигают неплохих результатов. Но чтобы быть действительно мощными, помимо прочего, они используют и статические упражнения для развития силы.
Что нужно знать о статике
С греческого языка статика – это равновесие. А статистические или изометрические – это упражнения, которые требуют удержания тела в неподвижном состояние за счет сопротивления силы тяжести.
Смысл статики в том, чтобы приложить максимально предельное усилие. Пытаясь сдвинуть с места условную кровать, вы скорее всего подвинете ее, и не приложите максимальную силу, а вот если вы попробуете сдвинуть камаз, что сделать в принципе невозможно, тогда вы затратите абсолютный максимум своих сил.
Виды статистических упражнений
Есть 3 типа изометрических упражнений:
1. Когда предельное мышечное напряжение противодействует непреодолимому сопротивлению.
2. Когда выполняя движение, совершаются остановки на пару секунд, создавая напряжение.
3. Когда создается помеха, останавливающая движения снаряда.
Статические упражнения заставляют мускулатуру испытывать предельное напряжение во время определённой фазы движения. Благодаря им вы повышаете силу мышц, которые у вас не очень хорошо проработаны.
Преимущества изометрических занятий
В отличие от динамического тренинга, статика тренирует силу для тех поз, в которых вы замираете, следовательно, для комплексного развития необходимо производить ротацию этих поз. То есть, динамические упражнения совершенствуют силу рывка, а изометрические развивают силу в целом. Но помимо этого, у статики есть ещё преимущества:
- Повышают крепость мышц и сухожилий
- Минимальные временные затраты
- Небольшой период восстановление мышц после тренировки
- Тренировки проводятся где угодно
- Используются любые прочные снаряды
- Развивают гибкость
При регулярных тренировках вы сделаете прочными сухожилия и в разы увеличите силовые показатели вашего тела.
Основные статические упражнения
Тренируйтесь где угодно и используйте что угодно. Например, вы можете толкать стену, пытаться согнуть металлический прут или разорвать цепь, включите фантазию и придумаете кучу вариантов для тренировки. Рассмотрим несколько упражнений для большего понимания:
- Используем дверной проём, упираемся в него ногами и руками и пытаемся оторвать косяк
- Берем палку и пытаемся её скрутить, имитируя отжим белья
- Ищем два дерева, которые расположены близко друг к другу, упираемся в одно спиной, а другое толкаем ногами
Данные упражнения выполняются дома или на улице. В тренажерном зале есть оборудование, благодаря которому вы можете делать гораздо больше упражнений, например:
- Статичный жим ногами
- Статичную вертикальную тягу
- Статичную становую тягу
- Статичный присед
Во время выполнения, не задерживайте дыхание, выполняйте одно упражнение не больше 12 секунд, между повторами отдыхаете примерно полминуты.
Если вы ни разу не включали в тренировки статику, то начините с элементарных движений, по мере возможности увеличивая нагрузку. Статические упражнения для развития силы помогут приобрести фантастическую форму, за небольшой временной отрезок.
Статическая сила — трение — Большая Энциклопедия Нефти и Газа, статья, страница 1
Статическая сила — трение
Cтраница 1
Статическая сила трения не зависит от размеров трущихся поверхностей. [1]
Статическая сила трения в зависимости от продолжительности неподвижного контакта возрастает до некоторого предела. Сила трения движения зависит от скорости скольжения поверхностей, причем соответственно давлению и — твердости сопряженных тел коэффициент трения может монотонно возрастать, убывать, переходить через максимум или минимум. [2]
Статическая сила трения не зависит от размеров трущихся поверхностей. [3]
[3]
Статическая сила трения Лпах
Статическая сила трения Fmax в достаточно широкие пределах не зависит от площади контакта соприкасающихся тел. При очень маленьких площадях контакта сила трения больше вследствие значительных деформаций поверхностей, которые имеют место в этом случае для реальных тел. [5]
Под статической силой трения ( трение покоя) понимают предельное значение силы трения, равное приложенной к нему внешней силе, приводящей в движение тело относительно поверхности, на которой оно находится. Иначе говоря, трением покоя называют такое значение силы трения, которое надо преодолеть для того, чтобы сдвинуть тело, находящееся в состоянии покоя. [6]
Под статической силой трения ( трение покоя) понимают предельное значение силы трения, равное приложенной к нему внешней силе, приводящей в движение тело относительно поверхности, па которой оно находится. Иначе говоря, трением покоя называют такое значение силы трения, которое надо преодолеть для того, чтобы сдвинуть тело, находящееся в состоянии покоя.
[7]
Иначе говоря, трением покоя называют такое значение силы трения, которое надо преодолеть для того, чтобы сдвинуть тело, находящееся в состоянии покоя.
[7]
В результате проведенного исследования получено выражение зависимостей статической силы трения торфа и высоты брикета от нагрузки. Константы этих выражений определяются физико-химическими и структурно-механическими свойствами материала. Разработана методика для комплексного изучения внешнего трения, деформации сжатия и фактической площади контакта волокнистых материалов. [10]
С целью исключения влияния на измеряемую величину статической силы трения различных побочных факторов
 Криволинейный характер зависимости ff ( P) для торфа объясняется значительной адгезией между торфом и стеклом.
[12]
Криволинейный характер зависимости ff ( P) для торфа объясняется значительной адгезией между торфом и стеклом.
[12]Моментом статических сопротивлений называется вращающий момент на валу рабочей машины, определяемый статическими силами трения, разрезания, скручивания, сжатия, растяжения, веса. [13]
Капля, растекаясь, преодолевает сопротивление движению периметра смачивания, которое можно обозначить как некоторую
Максимальное значение силы Fmax Qo, которую может развивать шероховатая плоскость, называется предельной или статической силой трения. Положение тела перед началом скольжения называют порогом скольжения. Сила трения, препятствующая относительному скольжению тела во время его движения, называется силой трения при движении. Опыт показывает, что сила трения при движении меньше статической силы трения Fmax. Если относительное скольжение тела отсутствует, то сила трения неопределенна: она может принимать любое значение от О до Fraax — Например, если тело малых размеров находится на плоскости в равновесии, то сила трения равна проекции равнодействующей активных сил на эту плоскость. Если проекция равнодействующей активных сил изменяется в пределах от О до Qo, то будет изменяться и сила трения, в то время как физические свойства плоскости остаются неизменными.
[15]
Опыт показывает, что сила трения при движении меньше статической силы трения Fmax. Если относительное скольжение тела отсутствует, то сила трения неопределенна: она может принимать любое значение от О до Fraax — Например, если тело малых размеров находится на плоскости в равновесии, то сила трения равна проекции равнодействующей активных сил на эту плоскость. Если проекция равнодействующей активных сил изменяется в пределах от О до Qo, то будет изменяться и сила трения, в то время как физические свойства плоскости остаются неизменными.
[15]
Страницы: 1 2
Выбор веревки
Благодарим Вас за Ваш выбор! По качеству своих веревок «АСКАН» относится к ведущим российским производителям аналогичной продукции, и широко известен среди альпинистов, промальпинистов и любителей активного отдыха по всей стране и странах СНГ. «АСКАН» предлагает веревки для спортивного лазания, для промышленного альпинизма и для спасательных работ, а так же канаты и шнуры самого широкого назначения.
Производственный комплекс «АСКАН» оснащен собственной испытательной лабораторией. Этот центр играет ключевую роль при разработке и производстве наших веревок. Новые модели веревки направляются в государственную испытательную лабораторию “СТАВАН-ТЕСТ” и “Институт Охраны Труда и промышленной безопасности” для проведения независимых испытаний, экспертиз и сертификации на соответствие как собственным “Техническим условиям”, так и международным стандартам EN 1891, EN 564.
Цель “АСКАНа”:
максимальное удовлетворение Вас — наших заказчиков!
Группы веревок
Веревки делятся, соответствии с назначением, на динамические, предназначенные для альпинистов, и статические (веревки страховочно-спасательные — ВСС), предназначенные для промышленных работ на высоте, для спасательных работ и в спелеологии, а также на веревки и шнуры технического назначения.
ОТЛИЧИЕ МЕЖДУ СТАТИЧЕСКОЙ, ДИНАМИЧЕСКОЙ ВЕРЕВКОЙ И ВСПОМОГАТЕЛЬНЫМ ШНУРОМ
Веревки с низким растяжением (EN 1891) обычно обозначаются как веревки статические. Они служат для страховки при работах на высоте, для спасательных работ, в спелеологии и пр. Важно, чтобы статическая веревка имела минимальное растяжение и максимальную прочность. Веревка альпинистская — динамическая (EN 892) — предназначена для страховки в тех случаях, когда при срыве есть риск падения на большую глубину. Ее задача — обеспечить минимальную нагрузку на человека даже при глубоком срыве за счет удлинения. Шнуры (EN 564) нельзя применять для страховки, а только для вспомогательных целей.
Они служат для страховки при работах на высоте, для спасательных работ, в спелеологии и пр. Важно, чтобы статическая веревка имела минимальное растяжение и максимальную прочность. Веревка альпинистская — динамическая (EN 892) — предназначена для страховки в тех случаях, когда при срыве есть риск падения на большую глубину. Ее задача — обеспечить минимальную нагрузку на человека даже при глубоком срыве за счет удлинения. Шнуры (EN 564) нельзя применять для страховки, а только для вспомогательных целей.
Что такое фактор срыва?
Динамические нагрузки на веревку при срыве зависят от высоты падения, длины выданной веревки и характеризуются фактором срыва (обозначаемый далее как f). Эта величина определяется соотношением:
высота падения (H)
f = ————————————-
рабочая длина веревки (L)
При срыве партнера в классической связке фактор срыва “f “, изменяется в пределах от 0 до 2,.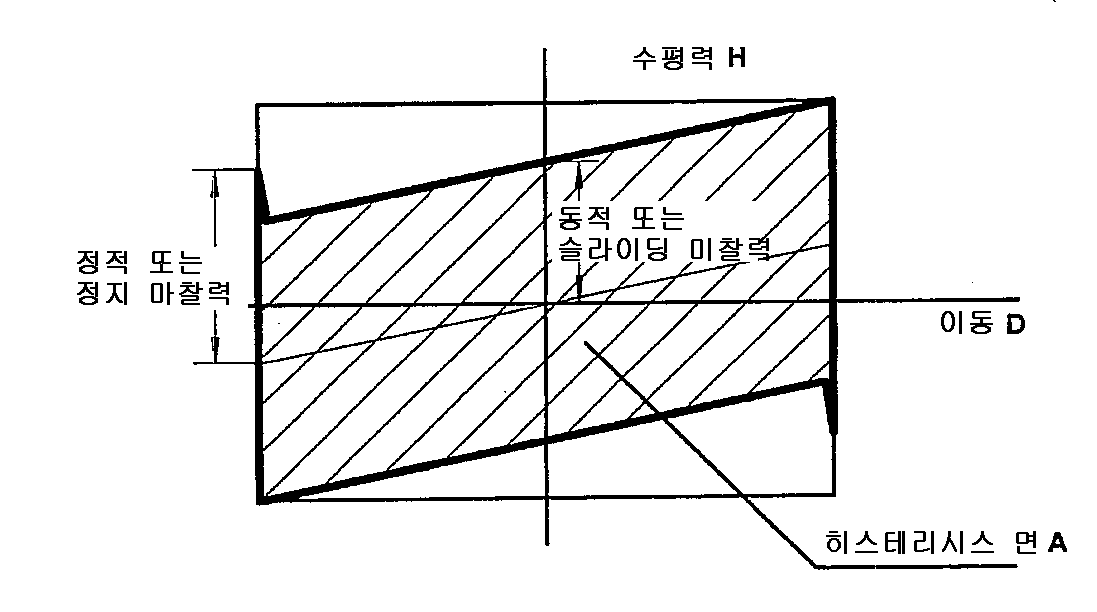 При прохождении так называемых «via ferrata», (применяется также название «klettersteig»), возможна ситуация, когда фактор падения будет иметь значение более 2. Речь идет о восхождении, когда Вы застрахованы короткой веревочной петлей, скользящей на карабине по стальному тросу. В случае падения, когда расстояние между точками крепления стального троса 5 м, а длина страховочной петли 1 м, то величина фактора срыва может достигнуть 7! Сила рывка, в этом случае, резко возрастает, что может привести к разрыву страховки или к тяжелым травматическим последствиям для альпиниста. Поэтому страховочные системы для «via ferrata» оборудованы встроенным амортизатором, который гасит силу рывка до 5 кН.
При прохождении так называемых «via ferrata», (применяется также название «klettersteig»), возможна ситуация, когда фактор падения будет иметь значение более 2. Речь идет о восхождении, когда Вы застрахованы короткой веревочной петлей, скользящей на карабине по стальному тросу. В случае падения, когда расстояние между точками крепления стального троса 5 м, а длина страховочной петли 1 м, то величина фактора срыва может достигнуть 7! Сила рывка, в этом случае, резко возрастает, что может привести к разрыву страховки или к тяжелым травматическим последствиям для альпиниста. Поэтому страховочные системы для «via ferrata» оборудованы встроенным амортизатором, который гасит силу рывка до 5 кН.
УДАРНАЯ СИЛА
Сила рывка зависит от конструкции веревки, фактора падения, веса альпиниста и способа страховки. Нужно иметь ввиду, что в течение срока эксплуатации и после рывков веревка теряет свои динамические качества и хуже гасит динамическую нагрузку при последующих срывах. Сила, действующая на последнюю точку страховки (крюк или закладку) при срыве является удвоенной силой рывка. Это должен помнить каждый альпинист при лазании с нижней страховкой.
Сила, действующая на последнюю точку страховки (крюк или закладку) при срыве является удвоенной силой рывка. Это должен помнить каждый альпинист при лазании с нижней страховкой.
КАК МОЖНО СНИЗИТЬ СИЛУ РЫВКА:
- организовать первую точку страховки как можно раньше, и тем самым снизить фактор падения,
- поддерживать низкий фактор падения по всему маршруту, организуя промежуточные точки страховки через малые интервалы.
- вести веревку через точки страховки свободно (с минимальным трением), так чтобы при срыве веревка могла растягиваться по всей выданной длине,
- использовать амортизаторы на промежуточных точках,
- не блокировать веревку при срыве партнера, для чего необходима тренировка и опыт.
ВНИМАНИЕ! Для страховки в тех случаях, когда при срыве есть риск падения на большую глубину, могут служить только динамические веревки, способные поглотить энергию падения. Ни в коем случае нельзя использовать для этой цели статические веревки, вспомогательные шнуры, лямочные петли! Даже неглубокий срыв на статической веревке может привести к критической силе воздействия на человека и точки страховки. Самостраховочную петлю рекомендуется делать из динамической веревки.
Самостраховочную петлю рекомендуется делать из динамической веревки.
Динамическая веревка
Динамическая веревка способна снизить усилие рывка при падении. Динамическая веревка (рис.2) изготавливается путем переплетения прядей проходящих по всей длине веревки без разрывов. Веревка имеет структуру: сердцевину (1), оплетку(2) и цветную нитью обозначающую год производства (3) внутри сердцевины. Материал для производства динамических веревок — полиамидное высокопрочное волокно.
Статическая веревка
Статические веревки — это плетенные капроновые веревки, конструкция которых подобна динамическим веревкам. Они также имеют сердцевину (1) и оплетку (2). Сердцевина имеет основную несущую функцию и состоит из отдельных прядей разной конструкции. Оплетка держит пряди вместе и защищает их от различных воздействий (механических, химических, тепловых и т. д.).
д.).
Внутри веревки находится цветная нить, обозначающая год производства (3). В настоящее время наша компания производит два типа статических веревок:
- веревки типа A (минимальная статическая разрывная нагрузка не менее 2200 кг.)
- веревки типа B (минимальная статическая разрывная нагрузка не менее 1800 кг.).
«АСКАН» производит все веревки и вспомогательные шнуры согласно “Техническим условиям” разработанными в соответствии требованиями европейских стандартов EN 1891 и EN 564.
Обозначение веревки
АСКАН обозначает концы клейкой лентой, на которой указан стандарт, согласно которого веревка произведена (EN 564 либо EN 1891), тип A либо B, материал из которого изготовлена веревка, название производителя. Если в процессе эксплуатации Вы самостоятельно разрезаете веревку, перенесите эту информацию на вновь образованные отрезки веревки любым доступным способом.
ЗНАЧЕНИЕ ОТДЕЛЬНЫХ СИМВОЛОВ
• ОДИНАРНЫЕ ВЕРЕВКИ
Часто для восхождения используется только одна одинарная веревка. Это наиболее распространенный способ использования веревок для восхождения.
• ДВОЙНЫЕОтдельные веревки крепятся попеременно в промежуточных точках. Такая система снижает риск повреждения веревок на камнеопасных участках маршрута.
• СДBОЕННЫЕ BЕРЕBКИИспользуются одинаковые веревки в паре, которые вместе простегиваются в карабины промежуточных точек страховки. Двойные веревки гарантируют высокую безопасность и наибольший ресурс по количеству срывов.
• СЕ — СИМВОЛ СООТВЕТСТВИЯДанный символ сообщает, что изделие отвечает требованиям безопасности, которые установлены соответствующей европейской нормой.
• EN 1891 Европейский стандарт, определяющий требования безопасности при тестировании веревок с низким растяжением (статических веревок) в рамках требований ЕС.
Европейский стандарт, определяющий требования безопасности при тестировании динамических альпинистских веревок в рамках требований ЕС.
• EN 566Европейский стандарт, определяющий требования безопасности при тестировании петель в рамках требований ЕС.
• EN 564Европейский стандарт, определяющий требования безопасности при тестировании вспомогательных альпинистских шнуров в рамках требований ЕС.
ISO Международная организация по стандартизации объединяет центры стандартизации всего мира. Норма ISO 9001 определяет правила всего процесса управления качеством. Данные нормы служат для обеспечения высокого качества изделий и услуг.
ИСПЫТАНИЕ АЛЬПИНИСТСКИХ ВЕРЕВОК ПО EN 892
ДИАМЕТР
Диаметр измеряется на веревке при нагрузке 10 кг у одинарной веревки, 6 кг — у половинок, и 5 кг — у двойных веревок.
МАССА
Указывается масса веревки на метр длины. Одинарная веревка без дополнительной обработки весит 52 — 88 грамм, половинка до 52 грамм, а двойная веревка до 42 грамм на метр.
КОЛИЧЕСТВО НОРМИРОВАННЫХ ПАДЕНИЙ
Указывается количество падений, которые должна выдержать веревка, при испытании по EN 892. B соответствии с этой нормой веревка должна выдержать не менее пяти срывов с f = 2 при 80 -ти килограммовом грузе. Половинка тестируются с грузом 55 кг. Двойные веревки с 80-ти килограммовым грузом. Испытываются всегда две веревки. Минимальное количество срывов с f = 2 — 12. Количество срывов является мерой безопасности (прочности) веревки. Ни одна новая веревка в хорошем состоянии при правильной эксплуатации — на практике, не может разорваться при указанной разрывной нагрузке. Постепенно из-за старения материала и износа, снижается ее прочность. Bлажность, воздействующая на волокна полиамида, также снижает прочность веревки.
МАКСИМАЛЬНАЯ СИЛА РЫВКА
Сила рывка — это мера динамического воздействия на человека при срыве, которая зависит от ряда условий (масса тела, фактор падения…). При испытаниях сила рывка в веревке растет с каждым следующим рывком и от этого зависит конечное число нормированных рывков. Чем выше число нормированных рывков, тем больше срок службы веревки.
Практическое воздействие на веревку в условиях реального восхождения и при испытании на стенде отличаются. При стандартном испытательном рывке конец веревки жестко
фиксируется, а в реальности всегда присутствует определенное проскальзывание веревки, это уменьшает силу рывка.
ВНИМАНИЕ! Величину силы рывка, в большой степени, определяет фактор падения, а не глубина срыва. При падении на глубину 5 м с фактором f = 1 сила рывка существенно меньше, чем при падении на ту же глубину с фактором f = 2. Энергию срыва принимает на себя т. н. «действующая длина веревки».
н. «действующая длина веревки».
СМЕЩЕНИЕ ОПЛЕТКИ
При испытаниях веревки измеряется, смещение оплетки относительно сердцевины. Норма EN 892 требует, чтобы смещение не превышало 20 мм при протягивании веревки длиной 1 930 мм, т.е. приблизительно ±1 %. При многократных подъемах по веревке на “жумарах” и при спусках по веревке возникает риск смещения оплетки.
УДЛИНЕНИЕ (СТАТИЧЕСКОЕ)
Относительное статическое удлинение измеряется при нагрузке веревки массой 80 кг. И не должно превышать 10 % у одинарных веревок и двойных (одновременно испытываются две веревки) и 12 % у «половинок» (испытывается одна веревка).
ДИНАМИЧЕСКОЕ УДЛИНЕНИЕ ПРИ ПЕРВОМ РЫВКЕ
Это удлинение веревки при первом нормированном испытательном рывке. Максимально допустимое динамическое удлинение 40 %, и этот параметр иллюстрирует свойства веревки лучше, чем статическая величина относительного удлинения.
Правильный выбор динамической веревки
ОДИНАРНЫЕ ВЕРЕВКИ
Веревки используются по одной там, где нет повышенной камнеопасности. Подходят для скальных восхождений, для скалодромов и для восхождений в классе «big walls». Одинарные веревки в большинстве своем диаметром от 9 мм и выше. С увеличением диаметром возрастает прочность веревки, количество допустимых рывков, но, к сожалению, и масса. Необходимо выбрать оптимальное соотношение между толщиной веревки и ее массой. Это определяется опытом, характером и стилем восхождения. Опытные альпинисты отдают предпочтение тонким и легким веревкам. Начинающим рекомендуют более толстую веревку, с большим запасом прочности Для длительных сложных восхождений необходимо найти компромисс между диаметром и весом веревки. Для лазания с верхней страховкой, т.н. «top rope» лазание, рекомендуется использовать специальные веревки, разработанные именно для этого — «indoor» веревки. Правильный выбор — залог Вашей безопасности и долгого срока службы веревки.
Правильный выбор — залог Вашей безопасности и долгого срока службы веревки.
ДВОЙНЫЕ ВЕРЕВКИ
Две веревки одного диаметра в паре, простегиваются вместе во все карабины промежуточных точек страховки. Применяются на технически сложных участках, которые могут встречаться не только в горах, но и на коротких скальных маршрутах.
ДВОЙНЫЕ ВЕРЕВКИ «ПОЛОВИНКИ»
Используя на восхождении «половинки», при которой «левая» и «правая» веревки идут параллельно в разные карабины промежуточных точек страховки, можно значительно повысить безопасность. Применение «половинок» позволяет снизить трение в карабинах, а также уменьшить силу рывка при падении. Одно из преимуществ «половинок» в возможности независимой работы каждой веревки. «Половинки» применяются в высоких горах, при сложном скальном лазании, в ледовых восхождениях и в смешанных рельефах (микстах).
ВНИМАНИЕ! Нельзя работать с двойной веревкой также как с «половинкой». Есть опасность пережигания веревки в карабине крепления из-за разной скорости перемещения прядей при срыве ведущего.
Есть опасность пережигания веревки в карабине крепления из-за разной скорости перемещения прядей при срыве ведущего.
Испытание веревок с малым удлинением (статических веревок) согласно EN 1891
ДИАМЕТРЫ ВЕРЕВОКДанная величина измеряется при нагрузке веревки весом 10 кг. Минимальный диаметр 8,5 мм, максимальный 16 мм.
УДЛИНЕНИЕ ВЕРЕВКИ
Статическое удлинение испытывается при испытательной нагрузке 150 кг (предварительное измерение при весе 50 кг). Должно быть не более 5 %.
СТАТИЧЕСКАЯ ПРОЧНОСТЬ
Всегда указывается на бирках веревок. В соответствии с требованиями EN 1891 веревки группы A имеют статическую прочность не менее 22 кН, у веревок группы В статическая прочность не менее 18 кН.
ВНИМАНИЕ! Рекомендованная рабочая нагрузка веревки — 1/10 номинальной прочности, указанной на этикетке изделия.
ТРЕБОВАНИЯ С ТОЧКИ ЗРЕНИЯ СВОЙСТВ МАТЕРИАЛА
Статическая веревка должна согласно EN 1891 изготавливаться из материала, который имеет точку плавления выше 195 °C. Для их изготовления нельзя использовать полиэтилен и полипропилен.
СМЕЩЕНИЕ ОПЛЕТКИ ОТНОСИТЕЛЬНО ЯДРА
У веревок типа A смещение на длине 2 м должно быть не более 40 мм (действует для веревок до диаметра 12 мм). У веревок типа B не должно превышать 15 мм.
ДИНАМИЧЕСКОЕ ВОЗДЕЙСТВИЕ
Методика и оборудование похожи на те, что используются при испытаниях динамики. Испытательный образец длиной 2 м. связан на концах узлами «восьмерка» и испытывается пятью рывками с фактором падения 1. Веревка должна выдержать все пять падений. Веревки тип A испытываются нагрузкой массой 100 кг. Веревка тип B испытывается весом 80 кг. Минимальное количество падения без разрыва веревки — пять.
ЖЕСТКОСТЬ ВЕРЕВКИ (УЗЛОВОЙ КОЭФФИЦИЕНТ)
Испытывается также как динамические веревки. В узел, затянутый при нагрузке в 10 кг, должна войти оправка диаметром не более чем в 1,2 раза больше диаметра веревки.
Выбор статической веревки
Веревки типа A имеют более высокую статическую и динамическую прочность, в этом их преимущество. Веревки типа B используются, например, в спелеологических экспедициях, когда необходимо экономить на весе снаряжения и экипировки. Персонал, работающий в промышленности со статическими веревками должен быть хорошо обучен. Веревки необходимо применять в соответствии с назначением, предохранять от возможных механических повреждений и воздействия агрессивных химических реагентов.
ВНИМАНИЕ! Закрепление статических веревок следует организовывать так, чтобы возможные срывы происходили с фактором падения не более чем f = 1!
Испытание вспомогательных шнуров
ДИАМЕТР
Вспомогательные шнуры испытываются подобно веревкам, только предварительная нагрузка ниже. Шнуры должны иметь согласно EN 564 диаметры 4, 5, 6, 7 и 8 мм. Меньшие диаметры 2, 3 мм — не испытываются.
Шнуры должны иметь согласно EN 564 диаметры 4, 5, 6, 7 и 8 мм. Меньшие диаметры 2, 3 мм — не испытываются.
ПРОЧНОСТЬ НА РАЗРЫВ
Минимальную прочность шнуров согласно EN 564 указывает следующая таблица:
| Диаметр | Минимальная прочность |
| 4мм | 3,2кН |
| 5мм | 5,0кН |
| 6мм | 7,2кН |
| 7мм | 9,8кН |
| 8мм | 12,8кН |
Сила мышц — информация для новичков 5Life
Сила мышц
Так просто, сразу сложно дать определение понятию сила мышц, потому что существует множество форм этой силы для той или иной функции.
Можно сказать, что сила мышц – это способность перемещать груз, преодолевая сопротивление, или поднимать вес, работая против земного притяжения, или растягивать пружину, превозмогая возникающие в ней силы упругости.
Выделяют максимальную мышечную силу, динамическую (или скоростную), статическую, а также отдельно силовую выносливость.
Для развития и наращивания силы мышц есть сенситивные периоды, то есть периоды, когда организм к таким занятиям наиболее готов и открыт. Специалисты считают, что у девочек такой период длится примерно с девяти до одиннадцати лет, у мальчиков с девяти до двенадцати и с четырнадцати до семнадцати. В этом возрасте у организма обнаруживаются благоприятные морфологические и функциональные условия.
Развитие силы мышц
Благодаря чему мускулы становятся более сильными, что делает мышцы сильнее? Сила мышц зависит от размера мускулов и от нервно-мышечной эффективности. Мышечная масса пополняется за счет поступления в организм белка, который является строительным материалом для мышц. Нервно-мышечная эффективность тренируется путем постоянных занятий на силовые упражнения. Мозг быстро обучается посылать сигналы о более сильном мышечном сокращении.
Как происходит развитие силы мышц? Как правильно тренироваться? Силовые упражнения разделяются на упражнения с внешним сопротивлением, на преодоление собственного веса и статические упражнения.
К первой группе относятся упражнения:
1. с подниманием тяжестей, тренажеры,
2. с партнером,
3. с упругими предметами (эспандерами, жгутами),
4. бег по местности с увеличенным сопротивлением (по песку, в гору, по снегу и так далее).
Для развития силовой выносливости хороши статические упражнения. Они не занимают много времени, не требуют специального оборудования и могут выполняться в ограниченном пространстве. Очень важно, что люди, занятые умственным трудом в офисах и учреждениях могут выполнять их без отрыва от производства.
Не удается найти страницу | Autodesk Knowledge Network
(* {{l10n_strings. REQUIRED_FIELD}})
REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings.TAGS}} {{$item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings. LANGUAGE}}
{{$select.selected.display}}
LANGUAGE}}
{{$select.selected.display}}{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}Методы исследования нервно-мышечного аппарата в практике гигиены труда
ПРИМЕНЕНИЕ ДИНАМОМЕТРИИ
Динамометрия представляет собой определение основных показателей произвольной дееспособности отдельных мышечных групп. К ним относятся максимальная произвольная сила (МПС), выносливость к статическим напряжениям и интегральный показатель – максимальная мышечная работоспособность (ММР).
К ним относятся максимальная произвольная сила (МПС), выносливость к статическим напряжениям и интегральный показатель – максимальная мышечная работоспособность (ММР).
Сила мышцы определяется наибольшим напряжением, которое она может развить. Основными измерительными приборами при этом являются различные виды динамометров – кистевые гидравлический и механический динамометры, ножной динамометр для измерения силы мышц – разгибателей спины. При измерении силы обследуемый осуществляет максимальное воздействие (плавно, без рывков) на соответствующее устройство динамометра. Достигнутая максимальная сила должна быть зафиксирована на 1 – 2 с.
Выносливость к статическому напряжению определяется по длительности периода, в течение которого обследуемый удерживает усилие, равное 75% от МПС. При измерении выносливости исследователь просит поддерживать заданное усилие максимально долго до отказа. Как только обследуемый достигает необходимого уровня усилия, исследователь включает секундомер и останавливает его в момент отказа поддерживать усилие. Срок удержания усилия (в секундах) и есть показатель статической выносливости.
Срок удержания усилия (в секундах) и есть показатель статической выносливости.
ММР определяется на основании двух измеренных динамометрических показателей как произведение силы на время удержания данной силы. При снижении работоспособности, развитии утомления динамометрические показатели, как правило, снижаются. Величина снижения статической выносливости является одним из показателей степени физического утомления при труде. Оптимальным в процессе обычного рабочего дня является снижение выносливости на 5 – 10%, предельно допустимым – на 20%. Превышение этого уровня указывает на развитие выраженного утомления НМА и служит основанием для проведения мероприятий по снижению трудовой нагрузки путем механизации и автоматизации трудовых операций, изменения норм труда (норм выработки, времени, численности рабочих и т. д.), рационализации режимов труда и отдыха.
ПРИМЕНЕНИЕ ТРЕМОРОМЕТРИИ
Треморометрия представляет собой регистрацию постоянных, непроизвольных мелких колебаний кисти и осуществляется с помощью специального прибора. Анализ треморометрии проводится по амплитуде и частоте колебаний. В используемом в практике гигиенических исследований электротремометре амплитуда отражается числом касаний краев фигурных пазов. При проведении измерений исследователь записывает показание счетчика электротремометра и включает его. По команде исследователя (при этом он запускает секундомер) обследуемый металлической указкой проводит через все фигурные пазы. После выполнения задания секундомер останавливается и вновь регистрируется показание счетчика. Разность в показаниях счетчика указывает количество касаний указкой краев паза. Делением значения общего числа касаний на время выполнения теста определяется частота – количество касаний в 1 с.
Анализ треморометрии проводится по амплитуде и частоте колебаний. В используемом в практике гигиенических исследований электротремометре амплитуда отражается числом касаний краев фигурных пазов. При проведении измерений исследователь записывает показание счетчика электротремометра и включает его. По команде исследователя (при этом он запускает секундомер) обследуемый металлической указкой проводит через все фигурные пазы. После выполнения задания секундомер останавливается и вновь регистрируется показание счетчика. Разность в показаниях счетчика указывает количество касаний указкой краев паза. Делением значения общего числа касаний на время выполнения теста определяется частота – количество касаний в 1 с.
При развитии утомления тремор усиливается, однако при трактовке результатов исследования необходимо учитывать влияние степени скоординированности напряжения мышц-антагонистов, а также степени скоординированности совместной деятельности зрительного и двигательного анализаторов.
ПРИМЕНЕНИЕ ЭЛЕКТРОМИОГРАФИИ
Электромиография (ЭМГ) – это регистрация биоэлектрической активности мышц, являющаяся одной из наиболее адекватных методик, позволяющих объективно оценить функциональное состояние НМА. В зависимости от характера отведения различают суммарную ЭМГ (отводится с помощью накожных электродов) и ЭМГ отдельных двигательных единиц (отведение осуществляется с помощью игольчатых электродов). В гигиенических исследованиях используется, как правило, суммарная ЭМГ. Она представляет собой результат сложения потенциалов действия ряда двигательных единиц, в состав которых входят мотонейрон, его аксон и несколько мышечных волокон. Задача исследователя сводится к отведению, усилению и регистрации этих потенциалов. Для этих целей используются электромиографы.
Статическая и динамическая работа мышц
Даже если человек находится в неподвижном положении, его мышцы все равно производят работу, поддерживая корпус и координируя тело в пространстве. В теле человека огромное количество мышц, объединенных в группы, которые работают слаженно, обеспечивая нормальную двигательную активность. Давайте узнаем, что такое статические и динамические мышцы, а также как использовать эти знания для грамотного тренинга. Много полезной информации по тренировкам и питанию вы узнаете в фитнес-клубе «Мультиспорт», где работают опытные специалисты, которые помогут вам достичь желаемых целей в фитнесе и спорте.
В теле человека огромное количество мышц, объединенных в группы, которые работают слаженно, обеспечивая нормальную двигательную активность. Давайте узнаем, что такое статические и динамические мышцы, а также как использовать эти знания для грамотного тренинга. Много полезной информации по тренировкам и питанию вы узнаете в фитнес-клубе «Мультиспорт», где работают опытные специалисты, которые помогут вам достичь желаемых целей в фитнесе и спорте.
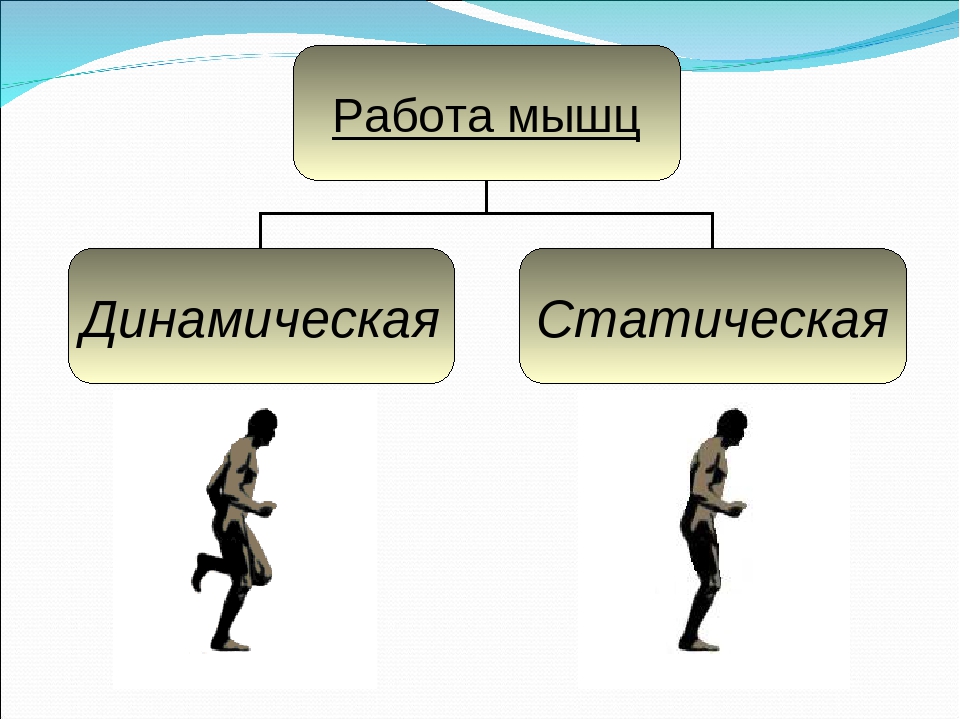
Виды работы мышц
Существует два вида работы мышц: статическая и динамическая. Если при работе мышц происходят движения в суставах, то ее называют динамической. Если суставы неподвижны, то работа мышц заключается в поддержании тела в определенном положении. В таком случае мышечную работу называют статической.
Легко понять, чем отличается динамическая и статическая работа мышц: в первом случае суставы совершают движение, во втором случае – остаются неподвижно. Теперь разберемся, чем характеризуется каждый вид работы.
Ключевой характеристикой динамичной работы мышц является энергозатратность. Несмотря на то, что мышцы тратят энергию в статике, во время активного движения ее затрачивается в разы больше.
Несмотря на то, что мышцы тратят энергию в статике, во время активного движения ее затрачивается в разы больше.
Динамическая работа мышц
Под динамической работой мышц подразумевается двигательная активность, при которой происходит попеременное расслабление и сокращение мышц для перемещения тела в пространстве или выполнения определенного движения.
При выполнении динамической работы происходят физиологические реакции организма, которых не возникает во время статической мышечной работы. Примером таких реакций служит увеличение пульса и артериального давления во время активности. Интенсивность проявления реакций зависит от разных факторов: тренированности человека, силы и частоты мышечного сокращения, и даже от того, в каком положении находилось тело до начала активности.
Динамическую работу классифицируют по количеству работающих мышц:
- Глобальная – если в движении принимают участие более двух третей от всех мышц тела;
- Региональная – если в движении задействовано менее двух третей от общего количества мышц;
- Локальная – если в движение участвует менее трети от всех мышц.

Например, базовые упражнения, вроде приседаний, становой тяги, прыжков задействуют огромное количество мышц, в результате чего происходит глобальная или региональная динамическая работа. Изолированные упражнения, например, подъем штанги на бицепс, разгибания на трицепс подключают в работу не слишком много мышц, а потому происходит локальная динамическая работа.
Динамическая работа мышц может быть преодолевающей и уступающей, что значит преодоление сопротивления и непротиводействие. Рассмотрим на примере мышц рук: при отведении выполняется преодолевающая динамическая работа, при приведении – уступающая. А при удержании руки в определенном положении выполняется статическая или удерживающая работа мышц.
Статическая работа мышц
Если вам интересно, какая работа мышц называется динамической и статической, то с первой уже разобрались. Динамическая работа возникает во время любого движения или физической активности. Теперь узнаем, какое отличие у статической работы.
При статической работе мышцы постоянно сокращаются, чтобы удерживать тело в определенном положении или обеспечивать выполнение простых бытовых действий.
При статической работе не происходит чрезмерного потребления кислорода и активации кровотока, но проявляются различные физиологические реакции и происходят энергетические затраты. Например, при выполнении статических упражнений, планки или стульчика тело тратит энергию на удержание определенного положения. Поэтому нагрузку мышц можно получить в статике, хотя энергозатраты, конечно, не сравнятся с динамической работой. Физиологические реакции организма в виде учащения пульса и повышения давления зависит от продолжительности работы и силы сокращений.
Между статической и динамической работой мышц есть различия, например, динамическая работа обеспечивается сокращающимися и расслабляющимися мышцами, а статическая – непрерывно сокращающимися. Но эти виды работы последовательно сменяют друг друга в нашей повседневной деятельности и не могут существовать друг без друга.
Что еще важно знать
В реальной жизни мышцы не работают изолированно, поэтому таблиц о конкретно динамической или статической работе вы не найдете. Важно помнить, что в статике всегда есть элементы динамики и наоборот.
Планируя тренировки на увеличение силы мышц, следует включать плиометрические и статические упражнения чтобы развивать медленные и быстрые мышечные волокна, что сделает вас сильнее и выносливее.
Многих интересует быстрое утомление мышц при статической нагрузке. Дело в том, что перманентное сокращение определенных мышц затрудняет насыщение клеток кислородом и выведение продуктов распада, что приводит к усталости. Во время динамических движений такого не происходит, поэтому поднимать и опускать руку вы можете дольше, чем удерживать ее в неподвижном положении.
Если вас интересует, что такое статические и динамические мышцы, а также как применить знания на практике, то приходите в клуб «Мультиспорт», где вас ждет множество интересных активностей, профессиональные тренеры, современно оборудованные залы и многое другое. Звоните прямо сейчас, чтобы получить подробную консультацию!
Звоните прямо сейчас, чтобы получить подробную консультацию!
Поделиться:
Статическое трение: определение, формула и примеры — видео и стенограмма урока
Что вызывает трение?
Если бы вы увидели очень крупный план гладкой поверхности, вы бы увидели, что на ней есть целый ландшафт с горами и долинами, ямами и ухабами. Эти недостатки приводят к тому, что две поверхности прижимаются друг к другу, что затрудняет скольжение предметов.
Но когда объект неподвижен, между двумя поверхностями также существует так называемое сцепление. Адгезия — это место, где две неподвижные поверхности слегка слипаются друг с другом из-за небольшой химической связи между материалами. Это то, что делает статическое трение таким сильным.
Неравенство статического трения
Сила — это толкающее или тянущее усилие, измеряемое в Ньютонах (Н). Трение — одна из таких сил. Мы можем вычислить, сколько Ньютонов силы трения существует между двумя поверхностями, используя это неравенство:
Коэффициент трения — это просто число, которое показывает, насколько две поверхности сцепляются друг с другом. Нормальная сила — это сила, которую поверхность прикладывает к объекту, чтобы удерживать его на поверхности. Без нормальной силы объекты провалились бы сквозь землю, потому что их было бы ничто не удерживать. На плоской поверхности эта нормальная сила равна силе тяжести, действующей на объект, и ее можно рассчитать, взяв массу объекта (в килограммах) и умножив ее на ускорение свободного падения:
Нормальная сила — это сила, которую поверхность прикладывает к объекту, чтобы удерживать его на поверхности. Без нормальной силы объекты провалились бы сквозь землю, потому что их было бы ничто не удерживать. На плоской поверхности эта нормальная сила равна силе тяжести, действующей на объект, и ее можно рассчитать, взяв массу объекта (в килограммах) и умножив ее на ускорение свободного падения:
Так, например, если блок стоит на склоне с коэффициентом трения 0.1, а нормальная сила, действующая на блок, составляет 2 Ньютона, мы можем использовать уравнение статического трения для расчета силы статического трения между откосом и поверхностью:
0,1 * 2 = 0,2 Ньютона
Уравнение статического трение почти идентично уравнению для других видов трения, например, кинетического трения. Единственное отличие состоит в том, что вместо коэффициента статического трения вы должны использовать коэффициент кинетического трения.
Почему сила статического трения выражается неравенством, а не уравнением? Представьте, что вы толкаете по полу очень тяжелую коробку.Вы толкаете все сильнее и сильнее, пока коробка, наконец, не начнет скользить. Сила статического трения отвечает за удержание коробки на месте. Когда вы немного толкаете, сила статического трения немного отступает. Когда вы нажимаете сильнее, сила статического трения отталкивает сильнее. Максимальное значение горизонтальной силы, которое вам потребуется для перемещения коробки, равно максимальному значению силы статического трения, которое равно произведению коэффициента статического трения и нормальной силы.Вот почему сила статического трения выражается неравенством. Оно может быть меньше или равно произведению коэффициента трения покоя и нормальной силы. Если вы нажмете сильнее, чем это, коробка начнет двигаться, сила статического трения больше не будет действовать на коробку, и сила кинетического трения возьмет верх.
Примеры статического трения
Статическое трение — это то, что не дает вашему автомобилю соскользнуть с холма при включенном стояночном тормозе. Это также то, что мешает вашей мебели двигаться при малейшем прикосновении.Вот почему ваша клавиатура имеет тенденцию прилипать к столу, если она остается на месте слишком долго. Фактически, всякий раз, когда вы пытаетесь переместить неподвижный объект, действует статическое трение.
Это также то, что мешает вашей мебели двигаться при малейшем прикосновении.Вот почему ваша клавиатура имеет тенденцию прилипать к столу, если она остается на месте слишком долго. Фактически, всякий раз, когда вы пытаетесь переместить неподвижный объект, действует статическое трение.
Краткое содержание урока
Статическое трение — это трение, которое существует между неподвижным объектом и поверхностью, на которой он покоится. Трение в целом — это сила, которая затрудняет скольжение двух объектов рядом друг с другом. Когда объекты уже начали движение, начинает действовать более слабое кинетическое трение , которое представляет собой трение, которое существует между двумя объектами, движущимися относительно друг друга.Вот почему заставить объект двигаться сложнее, чем удерживать его в движении. Статическое трение вызывается адгезией , легким химическим притяжением между двумя поверхностями. И трение, как правило, вызвано несовершенством каждой поверхности, сцепляемой и перекрывающей друг друга.
Силу статического трения можно рассчитать, взяв коэффициент трения между двумя поверхностями и умножив его на нормальную силу , которую поверхность прикладывает к объекту.На плоской поверхности нормальная сила равна силе тяжести, действующей на объект. Его можно рассчитать, умножив массу объекта (в килограммах) на ускорение свободного падения.
Трение | Физика
Цели обучения
К концу этого раздела вы сможете:
- Обсудите общие характеристики трения.
- Опишите различные типы трения.
- Рассчитайте величину статического и кинетического трения.
Трение — это сила, которая постоянно находится вокруг нас, которая препятствует относительному движению между системами, находящимися в контакте, но также позволяет нам двигаться (что вы обнаружили, если когда-либо пытались ходить по льду). Хотя это обычная сила, поведение трения на самом деле очень сложно и до сих пор полностью не изучено. Мы должны во многом полагаться на наблюдения, чтобы понять, какое понимание мы можем получить. Однако мы все еще можем разобраться с его более элементарными общими характеристиками и понять обстоятельства, в которых он себя ведет.
Мы должны во многом полагаться на наблюдения, чтобы понять, какое понимание мы можем получить. Однако мы все еще можем разобраться с его более элементарными общими характеристиками и понять обстоятельства, в которых он себя ведет.
Трение
Трение — это сила, которая препятствует относительному движению между контактирующими системами.
Одна из наиболее простых характеристик трения заключается в том, что оно параллельно поверхности контакта между системами и всегда в направлении, противоположном движению или попытке движения систем относительно друг друга. Если две системы находятся в контакте и движутся относительно друг друга, то трение между ними называется кинетическим трением . Например, трение замедляет скольжение хоккейной шайбы по льду.Но когда объекты неподвижны, между ними может действовать статическое трение , ; статическое трение обычно больше, чем кинетическое трение между объектами.
Кинетическое трение
Если две системы находятся в контакте и движутся относительно друг друга, трение между ними называется кинетическим трением.
Представьте, например, что вы пытаетесь сдвинуть тяжелый ящик по бетонному полу — вы можете толкать ящик все сильнее и сильнее, не двигая его вообще.Это означает, что статическое трение реагирует на ваши действия — оно увеличивается, чтобы быть равным вашему толчку и в противоположном ему направлении. Но если вы, наконец, достаточно сильно надавите, ящик, кажется, внезапно соскользнет и начнет двигаться. Находясь в движении, легче удерживать его в движении, чем начать, что указывает на то, что кинетическая сила трения меньше, чем сила статического трения. Если вы добавите массу в ящик, например, поставив на него коробку, вам нужно будет толкать еще сильнее, чтобы он начал, а также чтобы он продолжал двигаться.Более того, если вы смазываете бетон маслом, вам будет легче запустить ящик и продолжить работу (как и следовало ожидать).
Рисунок 1 представляет собой грубое графическое представление того, как возникает трение на границе между двумя объектами. Осмотр этих поверхностей крупным планом показывает, что они шероховатые. Поэтому, когда вы нажимаете, чтобы заставить объект двигаться (в данном случае ящик), вы должны поднимать объект до тех пор, пока он не сможет проскочить вместе с только кончиками поверхности, отломать точки или сделать и то, и другое.Существенной силе можно противостоять трением без видимого движения. Чем сильнее прижимаются поверхности друг к другу (например, если на ящик ставится еще одна коробка), тем больше силы требуется для их перемещения. Частично трение происходит из-за сил сцепления между поверхностными молекулами двух объектов, которые объясняют зависимость трения от природы веществ. Адгезия зависит от контактирующих веществ и представляет собой сложный аспект физики поверхности. Когда объект движется, остается меньше точек соприкосновения (меньше прилипающих молекул), поэтому требуется меньшая сила, чтобы удерживать объект в движении.На малых, но ненулевых скоростях трение практически не зависит от скорости.
Поэтому, когда вы нажимаете, чтобы заставить объект двигаться (в данном случае ящик), вы должны поднимать объект до тех пор, пока он не сможет проскочить вместе с только кончиками поверхности, отломать точки или сделать и то, и другое.Существенной силе можно противостоять трением без видимого движения. Чем сильнее прижимаются поверхности друг к другу (например, если на ящик ставится еще одна коробка), тем больше силы требуется для их перемещения. Частично трение происходит из-за сил сцепления между поверхностными молекулами двух объектов, которые объясняют зависимость трения от природы веществ. Адгезия зависит от контактирующих веществ и представляет собой сложный аспект физики поверхности. Когда объект движется, остается меньше точек соприкосновения (меньше прилипающих молекул), поэтому требуется меньшая сила, чтобы удерживать объект в движении.На малых, но ненулевых скоростях трение практически не зависит от скорости.
Рисунок 1.
Силы трения, такие как f , всегда противодействуют движению или попытке движения между соприкасающимися объектами.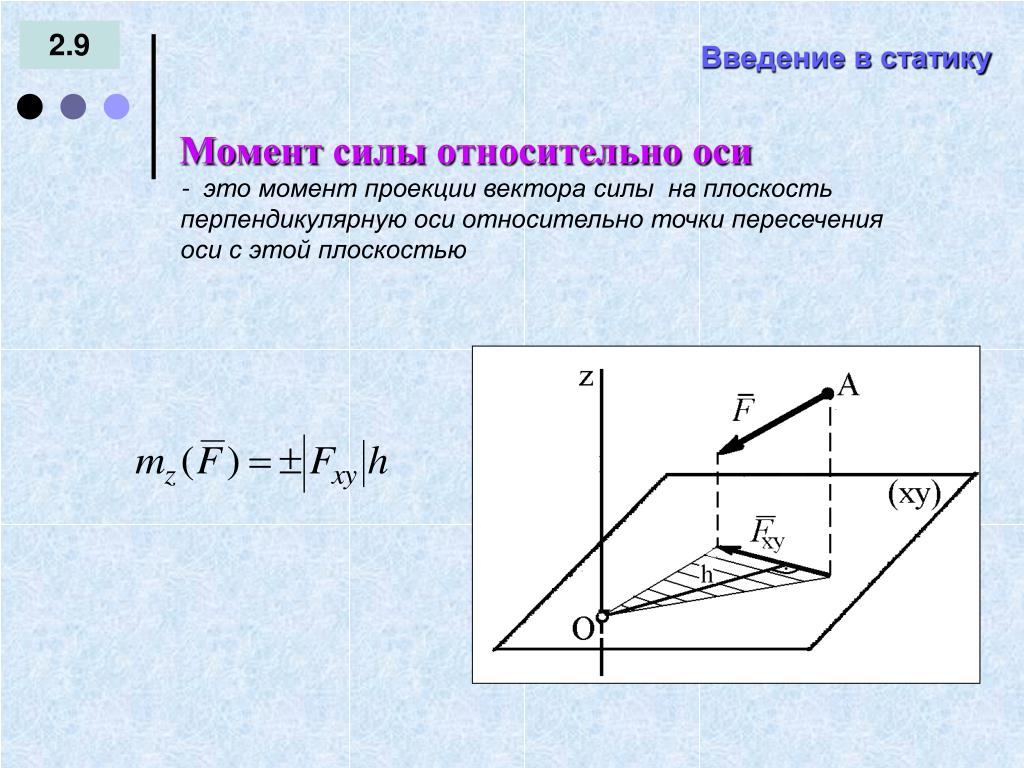 Трение возникает частично из-за шероховатости соприкасающихся поверхностей, как видно на увеличенном виде. Чтобы объект мог двигаться, он должен подняться до того места, где пики могут проскакивать по нижней поверхности. Таким образом, сила требуется только для того, чтобы привести объект в движение. Некоторые вершины будут сломаны, что также потребует силы для поддержания движения.Большая часть трения на самом деле возникает из-за сил притяжения между молекулами, составляющими два объекта, так что даже идеально гладкие поверхности не свободны от трения. Такие силы сцепления также зависят от веществ, из которых сделаны поверхности, что, например, объясняет, почему обувь с резиновой подошвой скользит меньше, чем обувь с кожаной подошвой.
Трение возникает частично из-за шероховатости соприкасающихся поверхностей, как видно на увеличенном виде. Чтобы объект мог двигаться, он должен подняться до того места, где пики могут проскакивать по нижней поверхности. Таким образом, сила требуется только для того, чтобы привести объект в движение. Некоторые вершины будут сломаны, что также потребует силы для поддержания движения.Большая часть трения на самом деле возникает из-за сил притяжения между молекулами, составляющими два объекта, так что даже идеально гладкие поверхности не свободны от трения. Такие силы сцепления также зависят от веществ, из которых сделаны поверхности, что, например, объясняет, почему обувь с резиновой подошвой скользит меньше, чем обувь с кожаной подошвой.
Величина силы трения имеет две формы: одну для статических ситуаций (статическое трение), другую для движения (кинетическое трение).
Когда нет движения между объектами, величина статического трения f s составляет f s ≤ μ s N , где μ s — это коэффициент трения покоя и Н, — величина нормальной силы (силы, перпендикулярной поверхности).
Величина статического трения
Величина статического трения f s is f s ≤ μ s N , где μ s — коэффициент статического трения, а N — величина нормальная сила.
Символ ≤ означает, что меньше или равно , подразумевая, что статическое трение может иметь минимальное и максимальное значение μ s N .Статическое трение — это реактивная сила, которая увеличивается, чтобы быть равной и противоположной любой приложенной силе, вплоть до своего максимального предела. Как только приложенная сила превысит f с (макс.) , объект переместится. Таким образом, f s (max) = μ s N .
Когда объект движется, величина кинетического трения f k определяется как f k = μ k N , где μ k — коэффициент кинетического трения. Система, в которой f k = μ k N описывается как система, в которой трение ведет себя просто .
Система, в которой f k = μ k N описывается как система, в которой трение ведет себя просто .
Величина кинетического трения
Величина кинетического трения f k определяется как f k = μ k N , где μ k — коэффициент кинетического трения.
Как видно из таблицы 1, коэффициенты кинетического трения меньше, чем их статические аналоги.То, что значения μ в Таблице 1 указаны с точностью до одной или, самое большее, двух цифр, является показателем приблизительного описания трения, даваемого двумя вышеупомянутыми уравнениями.
| Таблица 1. Коэффициенты статического и кинетического трения | ||
|---|---|---|
| Система | Статическое трение μ с | Кинетическое трение μ k |
| Резина на сухом бетоне | 1. 0 0 | 0,7 |
| Резина на мокром бетоне | 0,7 | 0,5 |
| Дерево по дереву | 0,5 | 0,3 |
| Вощеное дерево по мокрому снегу | 0,14 | 0,1 |
| Металл по дереву | 0,5 | 0,3 |
| Сталь по стали (сухая) | 0,6 | 0,3 |
| Сталь на стали (промасленная) | 0.05 | 0,03 |
| Тефлон на стали | 0,04 | 0,04 |
| Кость смазана синовиальной жидкостью | 0,016 | 0,015 |
| Туфли по дереву | 0,9 | 0,7 |
| Обувь на льду | 0,1 | 0,05 |
| Лед на льду | 0,1 | 0,03 |
| Сталь на льду | 0,4 | 0.02 |
Уравнения, приведенные ранее, включают зависимость трения от материалов и нормальной силы. Направление трения всегда противоположно направлению движения, параллельно поверхности между объектами и перпендикулярно нормальной силе. Например, если ящик, который вы пытаетесь толкнуть (с силой, параллельной полу), имеет массу 100 кг, то нормальная сила будет равна его весу: Вт = мг = (100 кг) ( 9,80 м / с 2 ) = 980 Н, перпендикулярно полу.Если коэффициент трения покоя равен 0,45, вам придется приложить силу, параллельную полу, более f s (макс.) = μ s N = (0,45) (980) N = 440N, чтобы переместить ящик. Когда есть движение, трение меньше, и коэффициент кинетического трения может быть 0,30, так что сила всего 290 Н f k = μ k N = (0,30) (980N) = 290N позволял ему двигаться с постоянной скоростью.Если пол смазан, оба коэффициента будут значительно меньше, чем без смазки. Коэффициент трения — это величина, на единицу меньше, с величиной обычно от 0 до 1,0.
Направление трения всегда противоположно направлению движения, параллельно поверхности между объектами и перпендикулярно нормальной силе. Например, если ящик, который вы пытаетесь толкнуть (с силой, параллельной полу), имеет массу 100 кг, то нормальная сила будет равна его весу: Вт = мг = (100 кг) ( 9,80 м / с 2 ) = 980 Н, перпендикулярно полу.Если коэффициент трения покоя равен 0,45, вам придется приложить силу, параллельную полу, более f s (макс.) = μ s N = (0,45) (980) N = 440N, чтобы переместить ящик. Когда есть движение, трение меньше, и коэффициент кинетического трения может быть 0,30, так что сила всего 290 Н f k = μ k N = (0,30) (980N) = 290N позволял ему двигаться с постоянной скоростью.Если пол смазан, оба коэффициента будут значительно меньше, чем без смазки. Коэффициент трения — это величина, на единицу меньше, с величиной обычно от 0 до 1,0. Коэффициент трения зависит от двух соприкасающихся поверхностей.
Коэффициент трения зависит от двух соприкасающихся поверхностей.
Эксперимент на вынос
Найдите небольшой пластиковый предмет (например, контейнер для еды) и поставьте его на кухонный стол, легонько постучав по нему. Теперь обрызгайте стол водой, имитируя легкий дождь.Что происходит теперь, когда вы нажимаете на объект одинакового размера? Теперь добавьте несколько капель (растительного или оливкового) масла на поверхность воды и дайте такой же кран. Что происходит? Это последнее обстоятельство особенно важно для водителей, особенно после небольшого ливня. Почему?
Многие люди испытывали скользкость при ходьбе по льду. Однако многие части тела, особенно суставы, имеют гораздо меньшие коэффициенты трения — часто в три или четыре раза меньше, чем у льда.Сустав образован концами двух костей, которые соединены толстыми тканями. Коленный сустав образован костью голени (большеберцовая кость) и бедренной костью (бедренная кость). Бедро представляет собой шарообразный (на конце бедренной кости) и суставную впадину (часть таза). Концы костей в суставе покрыты хрящом, который обеспечивает гладкую, почти стеклянную поверхность. Суставы также производят жидкость (синовиальную жидкость), которая снижает трение и износ. Поврежденный сустав или сустав с артритом можно заменить искусственным суставом (рис. 2).Эти заменители могут быть изготовлены из металла (нержавеющая сталь или титан) или пластика (полиэтилен), также с очень малым коэффициентом трения.
Концы костей в суставе покрыты хрящом, который обеспечивает гладкую, почти стеклянную поверхность. Суставы также производят жидкость (синовиальную жидкость), которая снижает трение и износ. Поврежденный сустав или сустав с артритом можно заменить искусственным суставом (рис. 2).Эти заменители могут быть изготовлены из металла (нержавеющая сталь или титан) или пластика (полиэтилен), также с очень малым коэффициентом трения.
Рис. 2. Замена искусственного колена — это процедура, которая проводится более 20 лет. На этом рисунке мы видим послеоперационные рентгеновские снимки замены правого коленного сустава. (Источник: Майк Бэрд, Flickr)
Другие природные лубриканты включают слюну, вырабатываемую во рту, чтобы помочь в процессе глотания, и скользкую слизь, находящуюся между органами в теле, позволяющую им свободно перемещаться друг мимо друга во время сердечных сокращений, во время дыхания и при движении человека.Искусственные лубриканты также распространены в больницах и врачебных клиниках. Например, когда выполняется ультразвуковое сканирование, гель, который соединяет датчик с кожей, также служит для смазывания поверхности между датчиком и кожей, тем самым уменьшая коэффициент трения между двумя поверхностями. Это позволяет датчику свободно перемещаться по коже.
Например, когда выполняется ультразвуковое сканирование, гель, который соединяет датчик с кожей, также служит для смазывания поверхности между датчиком и кожей, тем самым уменьшая коэффициент трения между двумя поверхностями. Это позволяет датчику свободно перемещаться по коже.
Пример 1. Упражнение на лыжах
Лыжник массой 62 кг спускается по снежному склону. Найдите коэффициент кинетического трения лыжника, если известно, что трение составляет 45.0 Н.
Стратегия
Величина кинетического трения была задана равной 45,0 Н. Кинетическое трение связано с нормальной силой N как f k = μ k N ; таким образом, коэффициент кинетического трения можно найти, если мы сможем найти нормальную силу лыжника на склоне. Нормальная сила всегда перпендикулярна поверхности, и поскольку нет движения перпендикулярно поверхности, нормальная сила должна равняться составляющей веса лыжника, перпендикулярной склону.(См. Диаграмму лыжника и свободного тела на рисунке 3.)
Диаграмму лыжника и свободного тела на рисунке 3.)
Рисунок 3.
Движение лыжника и трение параллельны склону, поэтому наиболее удобно проецировать все силы в систему координат, где одна ось параллельна склону, а другая перпендикулярна (оси показаны слева от лыжника). N (нормальная сила) перпендикулярна склону, а f (трение) параллельно склону, но w (вес лыжника) имеет составляющие вдоль обеих осей, а именно w ⊥ и W // .N равно по величине w ⊥ , поэтому движение перпендикулярно откосу отсутствует. Однако по величине f меньше W // , поэтому есть ускорение вниз по склону (по оси x ).
То есть N = w ⊥ = w cos 25º = мг cos 25º.
Подставляя это в наше выражение для кинетического трения, мы получаем f k = μ k mg cos 25º, что теперь может быть решено для коэффициента кинетического трения μ k . 2) (0,906)} = 0,082 \ [/ латекс].
2) (0,906)} = 0,082 \ [/ латекс].
Обсуждение
Этот результат немного меньше, чем коэффициент, указанный в таблице 5.1 для вощеной древесины на снегу, но он все же разумен, поскольку значения коэффициентов трения могут сильно различаться. В таких ситуациях, когда объект массой м скользит вниз по склону, который составляет угол θ с горизонтом, трение определяется как f k = μ k mg cos θ .В этих условиях все объекты будут скользить по склону с постоянным ускорением. Доказательство этого остается для задач и упражнений в этой главе.
Эксперимент на вынос
Объект будет скользить по наклонной плоскости с постоянной скоростью, если результирующая сила, действующая на объект, равна нулю. Мы можем использовать этот факт для измерения коэффициента кинетического трения между двумя объектами. Как показано в Примере 1, кинетическое трение на склоне f k = μ k mg cos θ. Компонент веса вниз по склону равен мг sin θ (см. Диаграмму свободного тела на рисунке 3). Эти силы действуют в противоположных направлениях, поэтому, когда они имеют одинаковую величину, ускорение равно нулю. Выписываем их:
Компонент веса вниз по склону равен мг sin θ (см. Диаграмму свободного тела на рисунке 3). Эти силы действуют в противоположных направлениях, поэтому, когда они имеют одинаковую величину, ускорение равно нулю. Выписываем их:
f k = Fg x
μ k мг cos θ = мг sin θ.
Решая для μ k , находим, что
[латекс] \ displaystyle \ mu _ {\ text {k}} = \ frac {mg \ sin \ theta} {mg \ cos \ theta} = \ tan \ theta \\ [/ latex]
Поместите монету в книгу и наклоните ее, пока монета не будет скользить по книге с постоянной скоростью.Возможно, вам придется слегка постучать по книге, чтобы монета сдвинулась с места. Измерьте угол наклона относительно горизонтали и найдите μ k . Обратите внимание, что монета вообще не начнет скользить, пока не будет достигнут угол, превышающий θ , поскольку коэффициент статического трения больше, чем коэффициент кинетического трения. Обсудите, как это может повлиять на значение μ k и его неопределенность.
Обсудите, как это может повлиять на значение μ k и его неопределенность.
Мы обсуждали, что когда объект опирается на горизонтальную поверхность, его поддерживает нормальная сила, величина которой равна его весу.Кроме того, простое трение всегда пропорционально нормальной силе.
Выполнение соединений: объяснение трения под микроскопом
Наиболее простые аспекты трения, о которых до сих пор говорилось, — это его макроскопические (крупномасштабные) характеристики. За последние несколько десятилетий в объяснении трения в атомном масштабе были достигнуты большие успехи. Исследователи обнаруживают, что атомная природа трения, по-видимому, имеет несколько фундаментальных характеристик. Эти характеристики не только объясняют некоторые из более простых аспектов трения — они также содержат потенциал для развития среды, почти свободной от трения, которая могла бы сэкономить сотни миллиардов долларов энергии, которая в настоящее время преобразуется (без необходимости) в тепло.
Рисунок 4 иллюстрирует одну макроскопическую характеристику трения, которая объясняется микроскопическими (мелкомасштабными) исследованиями. Мы отметили, что трение пропорционально нормальной силе, но не площади соприкосновения, что несколько противоречит здравому смыслу. Когда две шероховатые поверхности соприкасаются, фактическая площадь контакта составляет крошечную долю от общей площади, поскольку соприкасаются только высокие точки. Когда прикладывается большая нормальная сила, фактическая площадь контакта увеличивается, и обнаруживается, что трение пропорционально этой площади.
Рис. 4. Две соприкасающиеся шероховатые поверхности имеют гораздо меньшую площадь фактического контакта, чем их общая площадь. Когда нормальная сила больше в результате большей приложенной силы, площадь фактического контакта увеличивается, как и трение.
Но представление в атомном масштабе обещает объяснить гораздо больше, чем более простые особенности трения. Механизм генерации тепла сейчас определяется. Другими словами, почему при трении поверхности нагреваются? По сути, атомы связаны друг с другом, образуя решетки.Когда поверхность трутся, поверхностные атомы прилипают и заставляют атомные решетки вибрировать, по сути создавая звуковые волны, проникающие в материал. Звуковые волны уменьшаются с расстоянием, и их энергия преобразуется в тепло. Химические реакции, связанные с трением, также могут происходить между атомами и молекулами на поверхностях. На рисунке 5 показано, как острие зонда, проведенного по другому материалу, деформируется трением атомного масштаба. Сила, необходимая для перетаскивания наконечника, может быть измерена и, как выяснилось, связана с напряжением сдвига, которое будет обсуждаться позже в этой главе.Изменение напряжения сдвига замечательно (более чем в 10 12 ) и трудно предсказуемо теоретически, но напряжение сдвига дает фундаментальное понимание крупномасштабного явления, известного с древних времен — трения.
Другими словами, почему при трении поверхности нагреваются? По сути, атомы связаны друг с другом, образуя решетки.Когда поверхность трутся, поверхностные атомы прилипают и заставляют атомные решетки вибрировать, по сути создавая звуковые волны, проникающие в материал. Звуковые волны уменьшаются с расстоянием, и их энергия преобразуется в тепло. Химические реакции, связанные с трением, также могут происходить между атомами и молекулами на поверхностях. На рисунке 5 показано, как острие зонда, проведенного по другому материалу, деформируется трением атомного масштаба. Сила, необходимая для перетаскивания наконечника, может быть измерена и, как выяснилось, связана с напряжением сдвига, которое будет обсуждаться позже в этой главе.Изменение напряжения сдвига замечательно (более чем в 10 12 ) и трудно предсказуемо теоретически, но напряжение сдвига дает фундаментальное понимание крупномасштабного явления, известного с древних времен — трения.
Рис. 5. Наконечник зонда деформируется вбок под действием силы трения, когда зонд перемещается по поверхности. Измерения того, как сила изменяется для разных материалов, дают фундаментальное представление об атомной природе трения.
Измерения того, как сила изменяется для разных материалов, дают фундаментальное представление об атомной природе трения.
Исследования PhET: силы и движение
Узнайте, какие силы действуют, когда вы пытаетесь толкнуть шкаф для хранения документов. Создайте приложенную силу и посмотрите результирующую силу трения и общую силу, действующую на шкаф. На графиках показаны силы, положение, скорость и ускорение в зависимости от времени. Нарисуйте схему свободного тела всех сил (включая гравитационные и нормальные силы).
Нажмите, чтобы загрузить. Запускать на Java.
Сводка раздела
- Трение — это сила контакта между системами, которая препятствует движению или попытке движения между ними.Простое трение пропорционально нормальной силе N, толкающей системы вместе. (Нормальная сила всегда перпендикулярна поверхности контакта между системами.) Трение зависит от обоих материалов. Величина статического трения [латекс] {f} _ {\ text {s}} \\ [/ latex] между системами, неподвижными относительно друг друга, определяется как [латекс] {f} _ {\ text {s}} \ le {\ mu} _ {\ text {s}} N \\ [/ latex], где [latex] {\ mu} _ {\ text {s}} \\ [/ latex] — коэффициент статического трения, что зависит от обоих материалов.

- Кинетическая сила трения [латекс] {f} _ {\ text {k}} \\ [/ latex] между системами, движущимися относительно друг друга, определяется как [латекс] {f} _ {\ text {k}} = {\ mu} _ {\ text {k}} N \\ [/ latex], где [latex] {\ mu} _ {\ text {k}} \\ [/ latex] — коэффициент кинетического трения, который также зависит от обоих материалов.
Концептуальные вопросы
- Определите нормальную силу. Каково его отношение к трению, когда трение ведет себя просто?
- Клей на куске ленты может оказывать давление.Могут ли эти силы быть типом простого трения? Объясните, особенно учитывая, что лента может прилипать к вертикальным стенам и даже потолкам.
- Когда вы учитесь водить машину, вы обнаруживаете, что вам нужно немного отпустить педаль тормоза при остановке, иначе машина резко остановится. Объясните это с точки зрения взаимосвязи между статическим и кинетическим трением.
- Когда вы толкаете мел по классной доске, он иногда визжит, потому что он быстро то скользит, то прилипает к доске.
 Опишите этот процесс более подробно, в частности, объясните, как он связан с тем фактом, что кинетическое трение меньше статического. (Тот же процесс проскальзывания-захвата происходит, когда шины скрипят о тротуар.)
Опишите этот процесс более подробно, в частности, объясните, как он связан с тем фактом, что кинетическое трение меньше статического. (Тот же процесс проскальзывания-захвата происходит, когда шины скрипят о тротуар.)
Задачи и упражнения
Выразите свои ответы на проблемы в этом разделе с помощью правильного количества значащих цифр и правильных единиц.
- Специалист по физике готовит завтрак, когда замечает, что сила трения между его стальной лопаткой и тефлоновой сковородой составляет всего 0.200 Н. Зная коэффициент кинетического трения между двумя материалами, он быстро вычисляет нормальную силу. Что это?
- При ремонте двигателя своего автомобиля специалист по физике должен приложить 300 Н силы, чтобы вставить сухой стальной поршень в стальной цилиндр. а) Какова величина нормальной силы между поршнем и цилиндром? б) Какую величину силы ей пришлось бы приложить, если бы стальные детали были смазаны маслом?
- (a) Какова максимальная сила трения в коленном суставе человека, который поддерживает 66.
 0 кг ее массы на этом колене? (б) Во время интенсивных упражнений к суставам можно приложить усилия, которые легко в десять раз превышают поддерживаемый вес. Какова максимальная сила трения в таких условиях? Силы трения в суставах относительно малы при любых обстоятельствах, за исключением случаев, когда суставы ухудшаются, например, в результате травмы или артрита. Повышенные силы трения могут вызвать дальнейшие повреждения и боль.
0 кг ее массы на этом колене? (б) Во время интенсивных упражнений к суставам можно приложить усилия, которые легко в десять раз превышают поддерживаемый вес. Какова максимальная сила трения в таких условиях? Силы трения в суставах относительно малы при любых обстоятельствах, за исключением случаев, когда суставы ухудшаются, например, в результате травмы или артрита. Повышенные силы трения могут вызвать дальнейшие повреждения и боль. - Предположим, у вас есть деревянный ящик весом 120 кг, стоящий на деревянном полу.а) Какую максимальную силу вы можете приложить к ящику по горизонтали, не перемещая его? (б) Если вы продолжите прилагать эту силу после того, как ящик начнет скользить, какова будет величина его ускорения?
- (a) Если половина веса небольшого грузовика грузоподъемностью 1,00 × 10 3 кг поддерживается двумя его ведущими колесами, какова величина максимального ускорения, которого он может достичь на сухом бетоне? б) Будет ли металлический шкаф, лежащий на деревянной платформе грузовика, скользить, если он ускоряется с такой скоростью? (c) Решите обе проблемы, предполагая, что грузовик имеет полный привод.

- Бригада из восьми собак тянет сани с вощеными деревянными полозьями по мокрому снегу (месиво!). Собаки имеют среднюю массу 19,0 кг, а груженые сани с наездником имеют массу 210 кг. (a) Рассчитайте величину ускорения, начиная с состояния покоя, если каждая собака прилагает среднюю силу 185 Н назад к снегу. б) Какова величина ускорения, когда сани начинают двигаться? (c) Для обеих ситуаций рассчитайте величину силы сцепления между собаками и салазками.
- Рассмотрим фигуриста весом 65,0 кг, которого толкают двое других, показанных на рисунке 6. (a) Найдите направление и величину [латекса] {\ mathbf {F}} _ {\ text {tot}} \\ [/ latex ], общая сила, приложенная к ней другими, учитывая, что величины [латекс] {F} _ {1} \\ [/ латекс] и [латекс] {F} _ {2} \\ [/ латекс] равны 26,4 Н и 18,6 Н соответственно; (b) Каково ее начальное ускорение, если она изначально неподвижна и носит коньки со стальными лезвиями, которые указывают в направлении [latex] {\ mathbf {F}} _ {\ text {tot}} \\ [/ latex]? (c) Какое у нее ускорение, если предположить, что она уже движется в направлении [latex] {\ mathbf {F}} _ {\ text {tot}} \\ [/ latex]? (Помните, что трение всегда действует в направлении, противоположном движению или попытке движения между соприкасающимися поверхностями.
 )
)Рисунок 6.
- Покажите, что ускорение любого объекта вниз по склону без трения, который составляет угол θ с горизонталью, составляет a = g sin θ . (Обратите внимание, что это ускорение не зависит от массы.)
- Покажите, что ускорение любого объекта вниз по склону, где трение ведет себя просто (то есть, где f k = μ k N ), составляет a = g (sin θ — μ k cos θ ).Обратите внимание, что ускорение не зависит от массы и сводится к выражению, найденному в предыдущей задаче, когда трение становится пренебрежимо малым ( μ k = 0).
- Рассчитайте замедление снежной бордюры при подъеме на 5,0 ° с учетом коэффициента трения вощеной древесины по мокрому снегу. Результат вопроса 9 может быть полезен, но будьте осторожны, чтобы принять во внимание тот факт, что сноубордист едет в гору.
 Ясно покажите, как вы следуете шагам, указанным в Стратегиях решения проблем.
Ясно покажите, как вы следуете шагам, указанным в Стратегиях решения проблем. - (a) Рассчитайте ускорение лыжника, спускающегося по склону 10,0 °, принимая коэффициент трения для вощеной древесины по мокрому снегу. (b) Найдите угол наклона, под которым лыжник может двигаться по инерции с постоянной скоростью. Сопротивлением воздуха в обеих частях можно пренебречь, и вы найдете результат вопроса 9 полезным. Ясно покажите, как вы следуете шагам, указанным в Стратегиях решения проблем.
- Если объект должен стоять на склоне без скольжения, то трение должно равняться составляющей веса объекта, параллельной уклону.{-1} \ mu _ {\ text {s}} \\ [/ latex]. Вы можете использовать результат предыдущей задачи. Предположим, что a = 0 и статическое трение достигло своего максимального значения.
- Рассчитайте максимальное замедление автомобиля, движущегося под уклоном 6º (угол наклона 6º с горизонтом) при следующих дорожных условиях. Вы можете предположить, что вес автомобиля равномерно распределен на всех четырех шинах и что учитывается коэффициент статического трения, то есть шины не могут проскальзывать во время замедления.
 (Не обращайте внимания на прокатку.) Рассчитайте для автомобиля: (a) На сухом бетоне; б) на мокром бетоне; (c) На льду, при условии, что [latex] {\ mu} _ {\ text {s}} = 0,100 \\ [/ latex], то же самое, что и для обуви на льду.
(Не обращайте внимания на прокатку.) Рассчитайте для автомобиля: (a) На сухом бетоне; б) на мокром бетоне; (c) На льду, при условии, что [latex] {\ mu} _ {\ text {s}} = 0,100 \\ [/ latex], то же самое, что и для обуви на льду. - Рассчитайте максимальное ускорение автомобиля, движущегося вверх по склону 4º (тот, который составляет угол 4º с горизонтом) при следующих дорожных условиях. Предположим, что только половина веса автомобиля поддерживается двумя ведущими колесами и что учитывается коэффициент статического трения, то есть шины не могут проскальзывать во время ускорения.{5} N \\ [/ latex], если двигатели действуют одинаково? Это не большая сила трения для такой массивной системы. Трение качения поездов невелико, и, следовательно, поезда являются очень энергоэффективными транспортными системами. (b) Какова величина силы в соединении между 37-м и 38-м вагонами (это сила, которую каждый прилагает к другому), если предположить, что все автомобили имеют одинаковую массу и что трение равномерно распределено между всеми вагонами и двигатели?
- Рассмотрим 52.
 Альпинист с весом 0 кг на рис. 7. (a) Найдите натяжение веревки и силу, которую альпинист должен приложить ногами к вертикальной поверхности скалы, чтобы оставаться в неподвижном состоянии. Предположим, что сила прилагается параллельно ее ногам. Также предположим, что ее руки оказывают незначительное усилие; б) Каков минимальный коэффициент трения между ее туфлями и обрывом?
Альпинист с весом 0 кг на рис. 7. (a) Найдите натяжение веревки и силу, которую альпинист должен приложить ногами к вертикальной поверхности скалы, чтобы оставаться в неподвижном состоянии. Предположим, что сила прилагается параллельно ее ногам. Также предположим, что ее руки оказывают незначительное усилие; б) Каков минимальный коэффициент трения между ее туфлями и обрывом?Рис. 7. Часть веса альпиниста поддерживается веревкой, а часть — трением между ногами и скалой.
- Участник зимних видов спорта толкает 45.0-килограммовая глыба льда через замерзшее озеро, как показано на рисунке 8a. (a) Рассчитайте минимальную силу F, которую он должен приложить, чтобы заставить блок двигаться; б) Какова величина его ускорения, когда он начинает двигаться, если эта сила сохраняется?
Рис. 8. Какой метод скольжения ледяной глыбы требует меньшего усилия — (а) толкать или (б) тянуть под тем же углом относительно горизонтали?
- Повторите вопрос 18 с участником, который тянет ледяную глыбу с веревкой через плечо под тем же углом относительно горизонтали, как показано на рисунке 8b.

Глоссарий
трение: сила, противодействующая относительному движению или попыткам движения между системами, находящимися в контакте
кинетическое трение: сила, которая противодействует движению двух систем, которые находятся в контакте и движутся относительно друг друга
статическое трение: сила, которая противодействует движению двух систем, которые находятся в контакте и не движутся относительно друг друга
величина статического трения: [латекс] {f} _ {\ text {s}} \ le {\ mu} _ {\ text {s}} N \\ [/ latex], где [латекс] {\ mu} _ {\ text {s}} \\ [/ latex] — коэффициент статического трения, а N — величина нормальной силы.
величина кинетического трения: [латекс] {f} _ {\ text {k}} = {\ mu} _ {\ text {k}} N \\ [/ latex], где [латекс] {\ mu } _ {\ text {k}} \\ [/ latex] — коэффициент кинетического трения
Избранные решения проблем и упражнения
1. 5.00 N
5.00 N
4. (а) 588 с.ш .; (б) 1,96 м / с 2
6. (а) 3,29 м / с 2 ; (б) 3,52 м / с 2 ; (c) 980 N, 945 N
10. 1,83 м / с 2
14. (а) 4,20 м / с 2 ; (б) 2,74 м / с 2 ; (в) –0,195 м / с 2
16. а — 1.03 × 106 Н; (б) 3,48 × 105 Н
18. (а) 51,0 с.ш .; (б) 0,720 м / с 2
Сопротивление статическому трению будет соответствовать приложенной силе до порога движения.Тогда кинетическое сопротивление трения остается примерно постоянным. Этот график иллюстрирует стандартную модель трения. Приведенный выше график, хотя и представляет упрощенное представление о трении, довольно хорошо согласуется с результатами простых экспериментов с деревянными блоками на деревянных склонах. Экспериментальная процедура, описанная ниже, приравнивает компонент вектора веса вниз по склону к коэффициенту трения, умноженному на нормальную силу, создаваемую грузом на уклоне. Проведя этот эксперимент с большим количеством студентов, я могу сообщить, что полученный коэффициент статического трения почти всегда больше, чем коэффициент кинетического трения.Типичные результаты для древесины, которую я использовал, — 0,4 для статического коэффициента и 0,3 для кинетического коэффициента. Когда для измерения коэффициентов трения используются тщательно стандартизованные поверхности, разница между статическими и кинетическими коэффициентами имеет тенденцию исчезать, указывая на то, что разница может быть связана с неровными поверхностями, примесями или другими факторами, которые могут быть крайне невоспроизводимыми. Процитируем счетчик просмотров для указанной выше модели трения: | Индекс Концепции трения Ссылка |
Статическое и кинетическое трение
Статическое и кинетическое трениеСтатическое и кинетическое трение
Трение — ключевая концепция, когда вы пытаетесь разбираться в автомобильных авариях.Сила трения — это сила, сопротивляющаяся движению когда два объекта соприкасаются. Если вы посмотрите на поверхности всех предметов, есть крошечные шишки и гребни. Эти микроскопические пики и впадины улавливают один в другой, когда два объекта движутся мимо друг друга.
Это объяснение немного упрощено. Существуют и другие процессы, в том числе химическая связь и электрическая связь. взаимодействия.
Уровень трения, что разные материалы
Экспонат измеряется коэффициентом трения. Формула µ =
f / N, где µ — коэффициент трения, f — величина силы
сопротивляется движению, а N — нормальная сила. Нормальная сила — это сила при
какая одна поверхность проталкивается в другую. Если камень весом 50 ньютонов
лежит на земле, то нормальная сила равна 50 ньютонам силы. В
чем больше µ, тем больше сила сопротивляется движению, если два объекта скользят
мимо друг друга.
Формула µ =
f / N, где µ — коэффициент трения, f — величина силы
сопротивляется движению, а N — нормальная сила. Нормальная сила — это сила при
какая одна поверхность проталкивается в другую. Если камень весом 50 ньютонов
лежит на земле, то нормальная сила равна 50 ньютонам силы. В
чем больше µ, тем больше сила сопротивляется движению, если два объекта скользят
мимо друг друга.
Есть две формы трения, кинетическая и статический.Если вы попытаетесь сдвинуть два объекта друг с другом, небольшое количество силы не приведет к движению. Сила трения больше, чем приложенная сила. Это статическое трение. Если приложить немного больше силы, объект «вырывается на свободу» и скользит, хотя вам все равно нужно нанести сила, чтобы объект скользил. Это кинетическое трение. Вам не нужно приложить столько силы, чтобы удерживать предмет скольжения, сколько вам нужно изначально освобождаются от статического трения.
Некоторые общепринятые значения коэффициентов кинетической и статическое трение:
| Поверхности | µ (статика) | µ (кинетическая) |
| Сталь на стали | 0. | 0,57 |
| Стекло на стекле | 0,94 | 0,40 |
| Металл по металлу (со смазкой) | 0,15 | 0,06 |
| Лед на льду | 0.10 | 0,03 |
| Тефлон на тефлоне | 0,04 | 0,04 |
| Шина по бетону | 1,00 | 0,80 |
| Шина на мокрой дороге | 0.60 | 0,40 |
| Шина на снегу | 0,30 | 0,20 |
Эти значения являются приблизительными.
Теперь, наконец, как все это относятся к автомобилям?
В некоторых местах, особенно на Аляске в
зимой, вы должны постоянно держать в уме трение, когда едете, чтобы
чтобы избежать аварии.2)
V = начальная скорость автомобиля (м / сек)
µ = коэффициент трения между шинами и проезжей частью
Обратите внимание, что начальная скорость возведена в квадрат; это означает, что если вы путешествуете вдвое быстрее, ваш тормозной путь возводится в квадрат, не вдвое. Вот почему правило двух секунд («двигайтесь со скоростью, чтобы две секунды проходят между моментом, когда машина перед вами проезжает ориентир и момент, когда вы проезжаете тот же ориентир ») не действует для высоких скоростей; ваш тормозной путь увеличивается экспоненциально по мере того, как вы едете быстрее.
Чем выше коэффициент трения, тем меньше уменьшается
ваш тормозной путь. Поэтому лучше, чтобы ваша шина использовала статический
трение, а не кинетическое трение. Если шина катится так, что
поверхность, касающаяся земли, никогда не скользит, тогда действует статическое трение
чтобы замедлить машину. Если колеса заблокированы и скользят, то кинетическое трение
действует, чтобы замедлить машину. Чтобы использовать статическое трение, когда вам нужно
Чтобы быстро остановиться, есть несколько вариантов.Вы можете попытаться применить достаточно
тормоз, чтобы оставаться в статическом диапазоне трения и не слишком сильно, чтобы заблокировать
шины. Это лучший вариант с точки зрения максимально быстрой остановки, но он
может быть трудно быть настолько точным с тормозом. Это может быть особенно сложно
если вы собираетесь ударить лося. Другой вариант — прокачка тормоза, которая
имеет эффект чередования использования кинетического и статического трения в качестве
блокировка и разблокировка колес. Это не так эффективно, но проще сделать в
чрезвычайная ситуация.Последний вариант — поручить вашему автомобилю позаботиться о торможении в течение
вы, с помощью антиблокировочной системы тормозов или более сложных средств компьютерного управления.
Если шина катится так, что
поверхность, касающаяся земли, никогда не скользит, тогда действует статическое трение
чтобы замедлить машину. Если колеса заблокированы и скользят, то кинетическое трение
действует, чтобы замедлить машину. Чтобы использовать статическое трение, когда вам нужно
Чтобы быстро остановиться, есть несколько вариантов.Вы можете попытаться применить достаточно
тормоз, чтобы оставаться в статическом диапазоне трения и не слишком сильно, чтобы заблокировать
шины. Это лучший вариант с точки зрения максимально быстрой остановки, но он
может быть трудно быть настолько точным с тормозом. Это может быть особенно сложно
если вы собираетесь ударить лося. Другой вариант — прокачка тормоза, которая
имеет эффект чередования использования кинетического и статического трения в качестве
блокировка и разблокировка колес. Это не так эффективно, но проще сделать в
чрезвычайная ситуация.Последний вариант — поручить вашему автомобилю позаботиться о торможении в течение
вы, с помощью антиблокировочной системы тормозов или более сложных средств компьютерного управления. Антиблокировочная система тормозов делает то же самое, что и вы; прокачать тормоза. Лучшее решение
это, конечно, медленнее ехать.
Антиблокировочная система тормозов делает то же самое, что и вы; прокачать тормоза. Лучшее решение
это, конечно, медленнее ехать.
Путешествие по кривой заставляет вас испытать немного другой набор сил, так как вы должны иметь дело с тенденцией к машина хочет ехать прямо. Это объясняется 1-м законом Ньютона: объект не изменит скорость без силы, действующей на него.В таком случае, вы заставляете машину изменять поперечную скорость и двигаться в сторону, применяя сила трения от шин. Если у шин нет коэффициента трения достаточно большой, чтобы обеспечить силу, необходимую для бокового движения автомобиля, тогда вы скользить прямо вперед и съехать с дороги.
Обычно шины должны сохранять статическое трение для того, чтобы повернуть машину. Это ограничивает максимальную скорость до которые не скользят по шинам. Уравнение, моделирующее эту ситуацию:
Vmax = квадратный корень из ( µ (статический) г г)
Где:
Vmax = максимальная скорость
g = ускорение свободного падения (9. 2
* 10,0 м) = 5,4 м / сек, что составляет около 12,1 миль в час.
2
* 10,0 м) = 5,4 м / сек, что составляет около 12,1 миль в час.
задний
Новый закон трения для статической силы трения на основе локального проскальзывания предшественника
Приложение силы сдвига, превышающей максимальную силу статического трения, к ползуну на базовом блоке вызывает скольжение ползуна. Кинетическая сила трения действует на ползун в состоянии скольжения. Трение проявляется в различных системах от атомных до геологических масштабов и изучается с древних времен 1,2,3,4,5,6 .С инженерной точки зрения контроль трения имеет решающее значение для эффективного функционирования машин и может способствовать решению проблем в области энергетики и глобального потепления 4,5,6 . В 15 веке да Винчи обнаружил, что сила трения пропорциональна силе нагрузки и не зависит от видимой площади контакта между двумя твердыми объектами. Примерно 200 лет спустя Амонтоны заново открыли эти результаты, которые теперь все вместе называют законом Амонтона. Обычно считается, что этот закон применим для различных систем, обсуждается в школьных учебниках и используется для контроля трения в различных машинах.Отношение максимальной силы трения покоя к силе нагрузки называется коэффициентом трения покоя. Когда выполняется закон Амонтона, это соотношение является константой, которая не зависит от силы нагрузки или видимой площади контакта.
Обычно считается, что этот закон применим для различных систем, обсуждается в школьных учебниках и используется для контроля трения в различных машинах.Отношение максимальной силы трения покоя к силе нагрузки называется коэффициентом трения покоя. Когда выполняется закон Амонтона, это соотношение является константой, которая не зависит от силы нагрузки или видимой площади контакта.
Механизмы трения обычно объясняют следующим образом 1,2,3,4,5,6 . Шероховатость твердых поверхностей, контактирующих друг с другом, приводит к очень малой общей площади реальных точек контакта по сравнению с кажущейся площадью контакта. Реальные точки контакта дают конечную прочность на сдвиг на границе раздела, которая создается межатомными или межмолекулярными силами.Относительное скользящее движение между двумя контактирующими твердыми телами требует приложения силы сдвига, превышающей общую прочность на сдвиг, то есть должна быть приложена максимальная сила статического трения. Общая площадь реальных точек контакта называется реальной площадью контакта. Считается, что реальная площадь контакта пропорциональна силе нагрузки и не зависит от кажущейся площади контакта, а прочность на сдвиг на единицу реальной площади контакта постоянна. Таким образом, сила трения пропорциональна силе нагрузки, не зависит от видимой площади контакта и выполняется закон Амонтона.Обратите внимание, что на сегодняшний день также были предложены альтернативные схемы для объяснения механизмов трения и закона Амонтона 7 .
Считается, что реальная площадь контакта пропорциональна силе нагрузки и не зависит от кажущейся площади контакта, а прочность на сдвиг на единицу реальной площади контакта постоянна. Таким образом, сила трения пропорциональна силе нагрузки, не зависит от видимой площади контакта и выполняется закон Амонтона.Обратите внимание, что на сегодняшний день также были предложены альтернативные схемы для объяснения механизмов трения и закона Амонтона 7 .
В последнее время контактный интерфейс стал интересной темой в случае трения для силы сдвига, которая меньше макроскопической максимальной силы статического трения F s max , что соответствует началу скользящего движения для весь слайдер 8,9,10,11,12 . Массовое скольжение при этом не происходит.Мгновенная и локальная плотности реальной области контакта были измерены с использованием пропускания и отражения лазерного листа, демонстрируя, что локальное проскальзывание прекурсора происходит на границе контакта между ползуном из полиметилметакрилата (ПММА) и базовым блоком из ПММА 8 , 9,10,11,12 . Сила сдвига прикладывается к ползуну толкающим стержнем или пружиной на задней кромке ползуна. Фронт предвестника начинается от задней кромки ползуна и останавливается после прохождения определенного расстояния.Фронт следующего предвестника также начинается от задней кромки через определенный интервал и останавливается после того, как длина распространения больше, чем предыдущая длина. Первоначально длина распространения постепенно увеличивается с увеличением количества предшественников; однако после превышения критической длины длина распространения начинает быстро расти. Когда фронт прекурсора достигает передней кромки ползуна, происходит объемное скольжение. Такое поведение наблюдалось в различных экспериментах 8,9,10,11,12 , а скорость распространения фронта исследовалась в экспериментах 8,9,10,11 и в численных и теоретических исследованиях 12,13,14 , 15,16,17,18,19 .
Сила сдвига прикладывается к ползуну толкающим стержнем или пружиной на задней кромке ползуна. Фронт предвестника начинается от задней кромки ползуна и останавливается после прохождения определенного расстояния.Фронт следующего предвестника также начинается от задней кромки через определенный интервал и останавливается после того, как длина распространения больше, чем предыдущая длина. Первоначально длина распространения постепенно увеличивается с увеличением количества предшественников; однако после превышения критической длины длина распространения начинает быстро расти. Когда фронт прекурсора достигает передней кромки ползуна, происходит объемное скольжение. Такое поведение наблюдалось в различных экспериментах 8,9,10,11,12 , а скорость распространения фронта исследовалась в экспериментах 8,9,10,11 и в численных и теоретических исследованиях 12,13,14 , 15,16,17,18,19 .
Бен-Давид и др. экспериментально сообщил, что макроскопический коэффициент статического трения µ M = F s max / W , где W — сила нагрузки, сильно зависит от динамики предшественника 11 . С другой стороны, подходы метода конечных элементов (МКЭ) и аналитические расчеты были использованы, чтобы показать, что µ M уменьшается по мере увеличения давления и длины системы L 19 .Такое поведение определяется динамикой предшественника и квазистатическим переходом предвестника в быстрое движение на критической длине l c . В расчетах предполагается, что закон Амонтона выполняется локально, т.е. локальное напряжение трения пропорционально локальному давлению. Было получено следующее соотношение:
С другой стороны, подходы метода конечных элементов (МКЭ) и аналитические расчеты были использованы, чтобы показать, что µ M уменьшается по мере увеличения давления и длины системы L 19 .Такое поведение определяется динамикой предшественника и квазистатическим переходом предвестника в быстрое движение на критической длине l c . В расчетах предполагается, что закон Амонтона выполняется локально, т.е. локальное напряжение трения пропорционально локальному давлению. Было получено следующее соотношение:
, когда l c / L меньше единицы 19 . Здесь µ s и µ k — местные статические и кинетические коэффициенты трения соответственно.Зависимость l c от силы нагрузки дает новый закон трения:
, где a — константа, которая не зависит от W . Когда величина W и L такова, что l c / L близка к 0 или единице, закон Амонтона приблизительно выполняется. Вышеупомянутые зависимости были получены из аналитического расчета эффективной одномерной модели и подтверждены расчетом 2D FEM.Однако экспериментально эти результаты еще не подтверждены.
Вышеупомянутые зависимости были получены из аналитического расчета эффективной одномерной модели и подтверждены расчетом 2D FEM.Однако экспериментально эти результаты еще не подтверждены.
В этом исследовании мы экспериментально исследуем динамику прекурсора и макроскопический статический коэффициент трения ползуна из ПММА, загруженного на базовый блок из ПММА, используя пропускание лазерного листа. Обнаружено, что макроскопический коэффициент статического трения уменьшается с увеличением силы нагрузки. Экспериментальные результаты показывают слабую зависимость от скорости движения или высоты от поверхности контакта, к которой прикладывается тангенциальная сила пружины, которую мы называем поперечной силой.Результаты подтверждают соотношения (1) и (2) в пределах экспериментальной точности, то есть нарушение закона Амонтона и справедливость нового закона трения (Ур. (2). Также указывается, как эти отношения связаны с локальным проскальзыванием предвестника. Полученные здесь результаты согласуются с предыдущими экспериментальными исследованиями 20 , включая работу Ben-David et al. , указанный выше 11 . Более того, макроскопический коэффициент статического трения уменьшается по мере уменьшения видимой площади контакта.Этот результат также указывает на нарушение закона Амонтона.
, указанный выше 11 . Более того, макроскопический коэффициент статического трения уменьшается по мере уменьшения видимой площади контакта.Этот результат также указывает на нарушение закона Амонтона.
АНАЛИЗ СТАТИЧЕСКИХ СИЛ
АНАЛИЗ СТАТИЧЕСКИХ СИЛ6.2. АНАЛИЗ СТАТИЧЕСКОЙ СИЛЫ ОБОРУДОВАНИЯ
6.2.1 Системы без силы сопротивления
Сначала пренебрегаем силами, связанными с инерцией звеньев, и силами сопротивления. Позже мы включим силы сопротивления и рассмотрим эффекты инерции.
Анализ статических сил напрямую использует уравнения равновесия статических сил.Для формулировки аналитического решения необходимо нарисовать диаграмму свободного тела каждого твердого тела и определить неизвестные силы. Затем необходимо написать уравнения равновесия статических сил для каждого звена. Если выполнена правильная формулировка, результирующие уравнения будут равны количеству неизвестных компонентов силы, и эти уравнения будут линейными по отношению к неизвестным. Проиллюстрируем это на простом примере с четырьмя столбиками, показанном ниже:
Система находится в равновесии под действием внешней силы F 14 и T 12 .Величина и направление (h) силы F 14 известны. Нам необходимо определить T 12 и силы, действующие на суставы. На диаграммах свободного тела подвижных звеньев показано.
На диаграммах свободного тела показаны все неизвестные компоненты силы сустава (F ijx и F ijy ), действующие в положительных направлениях x и y. в результате получается отрицательное значение, это означает, что составляющая силы имеет обратную сторону.В показанном примере уравнения равновесия и равенства согласно третьему закону Ньютона (F ijx = -F jix ) приводят к 13 скалярным уравнениям с 13 неизвестными (T 12 , F 32x , F 32y , F 23x , F 23x , F 43x , F 43y , F 34x , F 34y , G 12x , G 12y , G 14x , G 14 ).
Для ссылки 2:
| Ф 32 года + G 12 лет = 0 | (SF y = 0) | (1) |
| F 32x + G 12лет = 0 | (SF x = 0) | (2) |
| F 32y a 2 cos (q 12 ) — F 32x a 2 sin (q 12 ) + T 12 = 0 | (SM A0 = 0) | (3) |
Для ссылки 3:
| F 23x + F 43x = 0 | (SF x = 0) | (4) |
| Ф 23 года + Ф 43 года = 0 | (SF y = 0) | (5) |
| F 43x a 3 sin (q 13 ) + F 34y a 2 cos (q 13 ) = 0 | (SM A = 0) | (6) |
Для ссылки 4:
| F 34x + G 14x -F 14 cos (h) = 0 | (SF x = 0) | 7) |
| F 34 года + G 14 лет -F 14 sin (h) = 0 | (SF y = 0) | (8) |
| F 34x a 4 sin (q 14 ) + F 34y a 4 cos (q 14 ) + F 14 r 4 (cos (h) sin ( q 14 ) -sin (h) cos (q 14 )) 0 | (SM B0 = 0) | (9) |
и за счет действия-противодействия (третий закон Ньютона):
| F 32 года = — F 23 года | (10) |
| F 32x = — F 23x | (11) |
| F 43 года = — F 34 года | (12) |
| F 43x = — F 34x | (13) |
Если анализ смещения выполняется заранее, e.грамм. если значения q 13 , q 14 определены для разных значений q 12 , приведенные выше уравнения можно использовать для каждого положения механизма. Еще один важный момент — это очень общая формулировка. Его можно использовать для механизмов, в которых несколько внешних сил действуют на одни и те же или разные звенья, а также в случаях, когда в суставах действуют силы сопротивления. Однако результирующее количество уравнений обычно слишком велико (если в механизме имеется -1 звеньев, то будет 3 (-1 -1) уравнения равновесия).
Можно уменьшить количество решаемых уравнений, если проанализировать диаграммы свободного тела до некоторой степени. Нет необходимости записывать силы в терминах их компонентов x и y, если направление известно, и можно определить силы, которые имеют равную величину, прежде чем пытаться найти решение. Схемы свободного тела звеньев четырехзвенного механизма перерисованы ниже.
В этом случае для упрощения расчетов отметим, что F ij = -F ji для совместных сил.Кроме того, поскольку звено 3 является двухсиловым элементом, F 23 и F 43 равны, противоположны, и их линия действия проходит вдоль AB. Следовательно, F 23 = F 23 q 13 , а q 13 известно из кинематического анализа. Кроме того, звено 2 представляет собой элемент с двумя усилиями и моментом. Следовательно:F 13 = — G 12
Отсюда:
F 43 = -F 32 = -F 34 = -G 12 = -F 23
Теперь можно найти неизвестные силы, если мы напишем 3 уравнения равновесия для звена 4 и уравнение равновесия с одним моментом для звена 2, которые равны
— F 14 cosh + F 34 cosq 13 + G 14 cosf = 0 или F 14 cosh + F 34 cosq 13 + G 14x = 0
— F 14 sinh + F 34 sinq 13 + G 14 sinf = 0 или F 14 cosh + F 34 cosq 13 + G 14y = 0
r 4 F 14 (cosh sinq 14 — sinh cosq 14 ) + a 4 F 34 (sinq 13 cosq 14 — cosq 13 sinq7 ) = 0
и
a 2 F 32 (cosq 13 sinq 13 -sinq 13 cosq 12 ) + T 12 = 0 ( Факс 32 = — Факс 34 )
Есть четыре уравнения с четырьмя неизвестными (F 34 , T 12 , G 14 , f или F 34 , T 12 , G 14x , G 14y ).Если значения оказываются отрицательными, направление силы или крутящего момента противоположно указанному на диаграмме свободного тела. Если обобщить приведенный выше результат, мы увидим, что:
a) Для двухсиловых элементов вам не нужно писать уравнения равновесия. Вы можете просто указать, что силы равны и противоположны, и их линия действия совпадает с линией, соединяющей точки приложения.
b) Для элементов с двумя усилиями и моментом вы должны написать только уравнение равновесия момента.Две силы равны и противоположны, и они образуют пару, равную и противоположную приложенному моменту.
c) В случае трех или четырех силовых элементов должны быть записаны три уравнения равновесия (SF x = 0, SF y = 0, SM = 0).
Еще одно упрощение в решении уравнений моментного равновесия получится, если мы воспользуемся единичным вектором в направлении сил и запишем вектор силы в форме
F = F v
Где F — величина F , а v — единичный вектор в направлении силы F .
Аналогичным образом мы можем представить вектор положения r как:
r = r u
Где r — расстояние от точки C до точки на линии действия F , а u — единичный вектор в направлении r . Момент силы F вокруг оси, проходящей через 0 и перпендикулярной плоскости, будет:
M = rxF = r u xF v = rF ( uxv )
с
u = 1 a = cos a i + sin a j ;
v = 1 b = cos b i + sinb j
u x v = (sin b cos a — cos b sin a) k
или:
u x v = sin (b- a) k
Следовательно M = rxF = r F sin (b — a) k
Теперь перерисованы диаграммы свободного тела из предыдущего примера.
Уравнения моментного равновесия:
a 4 u 4 x F 34 u 3 + r 4 u 4 x (-F 14 ) v 1 (S B0 = 0)
a 2 u 2 x (-F 32 ) u 3 + T 12 k = 0 (SM A0 = 0)Что дает:
a 4 F 34 sin (q 13 -q 14 ) — r 4 F 14 sin (h-q 14 ) = 0
-a 2 F 32 sin (q 13 -q 12 ) + T 12 = 0
Видно, что приведенные выше уравнения — это точно такие же уравнения, которые мы получили ранее.
Если бы мы решали уравнения равновесия графически, обратите внимание, что звено 4 является трехсиловым элементом, и силы должны быть параллельными. Поскольку линия действия силы F 34 , а также величина и направление F 14 известны, точка совпадения находится на пересечении линий действия этих двух сил. Следовательно, линия действия G 14 — линия, соединяющая B 0 с точкой параллелизма. Далее можно нарисовать многоугольник силы:
Факс 14 + Факс 14 + Факс 34 = 0
Мы хотим определить величины сил G 14 и F 34 .Для этого сила F 14 рисуется в виде вектора линии, длина которого пропорциональна величине силы за счет использования определенного масштаба силы (kf мм / Н). Поскольку F 43 = -F 34 (третий закон Ньютона), F 23 = -F 43 (равновесие двух силовых элементов), F 32 = -F 23 (третий закон Ньютона) и G 12 = -F 32 (равновесие двухсилового и моментного элемента), все совместные силы определены.Чтобы определить крутящий момент T 12 , можно измерить перпендикулярное расстояние h от точки A 0 до линии действия F 32 и T 12 = hxF 32 . Направление входного крутящего момента должно быть противоположным моменту пары, создаваемой F 23 и G 12 . Полученные в результате диаграммы свободного тела и силовой многоугольник выглядят следующим образом:
В качестве другого примера рассмотрим кривошипно-ползунковый механизм, показанный
..Система находится в статическом равновесии для всех углов поворота коленчатого вала под действием известной силы F 14 , действующей на звено 4, и неизвестного крутящего момента T 12 , действующего на звено 2. Мы должны определить совместные усилия и входной крутящий момент, T 12 .
Обратите внимание, что звено 3 — это две силы, звено 2 — это две силы и момент. В случае звена 4 существует известная внешняя сила F 14 , сила шарнира F 34 , направление которой известно (вдоль AB).Должна быть сила шарнира G 14 (перпендикулярно оси ползуна) и момент M 14 (перпендикулярно плоскости) из-за действия звена 1 на звено 4. Твердое тело находится в равновесии под действием трех сил и момента.Сила G 14 может быть размещена в любом месте на звене 4. Поскольку звено 4 находится в статическом равновесии, это изменит величину момента M 14 .Если линия действия G 14 проходит через точку пересечения F 14 и F 34 , момент M 14 будет равен нулю и твердое тело будет в равновесие под действием трех сил. Если точка совпадения, O, трех сил лежит в пределах физических границ скользящего соединения, будет иметь место контакт поверхности между звеньями 1 и 4. (На рисунке контакт находится в точке нижняя поверхность. Если направление G 14 направлено вниз, а не вверх, контакт будет на верхней поверхности) и звено 4 не будет подвергаться вращательному движению внутри ползуна.Однако, если точка совпадения O находится за пределами границ (b), сила G 14 является фиктивной силой, которая является равнодействующей сил, действующих в области контакта (из-за равновесия под действием трех сил: G 14 + F 34 + F 14 = 0).
(a) Точка параллелизма находится в пределах совместной границы (b) Точка параллелизма за пределами совместной границы
Физически совместные силы должны возникать из-за действия и противодействия между двумя контактирующими поверхностями на двух разных звеньях.В случаях, показанных на рисунке (b), поскольку силы, действующие на звено 4, стремятся вращать звено 4, если мы предполагаем полную жесткость звеньев, звенья 1 и 4 будут в точечном контакте на двух краях границ, как показано В точках контакта будут действовать совместные силы G’14 и G’14, направления которых перпендикулярны оси ползуна (на самом деле эти силы будут перпендикулярны общей касательной между двумя контактирующими поверхностями. В обычных системах машин, поскольку зазор в шарнир мал по сравнению с размерами соединения, угловое вращение незначительно, и это предположение действительно).
Также обратите внимание, что:
G 14 = G ’ 14 + G” 14 (По величине G 14 = G ’ 14 — G” 14 для показанного случая)
G « 14 d = G ‘ 14 b
G 14 может иметь очень малую величину, в то время как фактические контактные силы G ’ 14 и G” 14 могут быть значительными.
Если вас интересует только равновесие сил, любая из диаграмм равновесия для звена 4 будет правильной и действительной. Однако, если вас интересуют фактические совместные усилия, необходимо определить тип контакта и фактические величины сил в точке (ах) контакта. Это также будет иметь важное значение, когда необходимо учитывать трение в этих соединениях. Величины G ’ 14 и G” 14 будут зависеть от геометрии соединения, а также от величины и направления других сил, действующих на звено.Также обратите внимание, что в течение одного цикла механизма тип контакта между звеньями 1 и 4 изменится. Как показано, будет четыре различных режима контакта (G 14 = — G 41 ). Обратите внимание, что величины всех сил и размеров должны быть положительными для всех четырех режимов. В противном случае механизм не находится в предполагаемом режиме контакта.
Режимы контакта для призматического соединения
Пример 6.1.
На рисунке показан механизм быстрого возврата Whithworth. Мы хотим определить крутящий момент и совместные усилия, когда предполагается, что система находится в статическом равновесии, когда входной угол поворота коленчатого вала q 12 = 30 0 . После выполнения кинематического анализа (графического или аналитического) в показанном положении переменные положения имеют следующие значения:B 0 A = 158,75 мм; q 14 = 49.11 0 B 0 C = 285,13 мм; q 15 = 169,55 0
Схема каждого звена со свободным телом показана выше. Отметим, что звенья 3 и 5 являются двухсиловыми, а звено 2 — двухсиловым плюс момент. Для звена 6, если мы предположим, что между звеньями 1 и 6 существует единая совместная сила, мы отметим, что точка совпадения и результирующая совместная сила, G 16 , находится за пределами границ точек контакта и режим III.
У нас есть:
F 56 = — F 65 = F 45 = -F 54
F 34 = — F 43 = F 23 = -F 32 = G 12
F 56 = — F 56 u 5 где u 5 = 1 0 = cos (169.95 0 ) i + sin (169.95 0 ) jF 16 = -100 i (N)
G ” 16 = G” 16 j и G ’ 16 = -G’ 16 j
Силовое равновесие звена 6, результаты:
(G ” 16 — G’ 16 ) j — F 56 u 5 — 100 j = 0
или
(G ” 16 — G’ 16 ) — F 56 sin (169.95 0 ) = 0
— F 56 cos (169,95 0 ) -100 = 0
Уравнение моментного равновесия (SM C = 0) дает (расстояние от точки B до двух границ составляет 70 и 30 мм соответственно. Эти расстояния будут зависеть от положения механизма):
G ’ 16 * 70 + G” 16 * 30-100 * 20 = 0
Получаем:
Факс 56 = 101.56 N 0; G ’ 16 = 14,68 N 0; G ” 16 = 32,41 N 0
Так как звено 5 является двухсиловым элементом F 54 = -F 45 = F 65 = -F 56 = 107,56 Н 0.
Уравнение равновесия сил для звена 4:
F 54 u 5 + G 14 v 4 + F 34 u 3 = 0
Где
v 4 = 1 f = cosf i + sinf j
u 3 = 1 q14 -90 0 ) = cos 40.89 0 i — sin 40,89 0 j
Уравнения силового равновесия также можно записать в виде:
F 54 cos 169,95 0 + G 14 cosf + F 34 cos 40,89 0 = 0
F 54 sin l69.95 0 + G 14 sin f-F 34 sin 40,89 0 = 0
Уравнение моментного равновесия (SM B = 0):
a 4 u 4 x F 54 u 5 + r 4 u 4 x F 34 u 3 5 = 0
Где:
u 4 = 1 q 14 = cos 49.11 0 i + sin49.11 0 j
и
B 0 B = a 4 = 60 мм, B 0 A = r 4 = 158,75 мм
Когда уравнение моментного равновесия упрощается:
a 4 F 54 sin (q 15 -q 14 + r 4 F 34 sin (q 14 -90 0 -q 14 ) = 0
или:
a 4 F 54 sin (120.44 0 ) — r 4 F 34 = 0
F 34 = 33,14 N 0 , G 14 = 75,02 N 0
Для ссылки 2:
F 32 = 33,14 N 0
G 12 = 33,14 N 0
И уравнение равновесия моментов дает:
Т 12 + 120 * 33.14 sin (139,11 0 -30 0 ) = 0
или
T 12 = -3757,65 Н-мм
или
Т 12 = 3,76 Н-м (по часовой стрелке)
Пример 6.2.
Рассмотрим представленный пневматический пресс. Это шестизвенный механизм. Усилие F 16 , прикладываемое обрабатываемой деталью к толкателю (звено 6), приводится в равновесие за счет пневматического давления, приложенного к поршню и цилиндру.
Рассмотрим схемы подвижных звеньев свободного тела. Когда звено 6 рассматривается как элемент с тремя силами, точкой параллелизма является точка C, которая находится за пределами границ скользящего соединения. G 16 — это фиктивная сила, которая является равнодействующей G ‘ 16 и G « 16 . Мы можем написать:
Факс 56 + Факс 16 + G 16 = 0
G ‘ 16 -G « 16 = G 16
AG ‘ 16 = cG « 16
Если F 16 и положение механизма известно, приведенные выше уравнения можно использовать для определения G ‘ 16 , G « 16 и F 16
Когда мы рассматриваем звено 5, поскольку в B между звеньями 4,5 и 3 имеется тройное соединение, мы должны знать, как это соединение построено.
Как показано выше, либо штифт может быть жесткой частью одного из звеньев (скажем, звено 3), а другие звенья (4 и 5) соединены с этим звеном (в этом случае нет соединения между звеньями 4 и 5). ), либо штифт представляет собой отдельное свободное тело, к которому подключены все три звена. Когда степень стыка больше единицы, обычно рассматривают диаграмму свободного тела пальца. Штифт B будет находиться под действием трех одновременных сил F 3B , F 4B , F 5B ( F 3B + F 4B + F 5B = 0 ).Теперь, когда мы рассматриваем звенья 4 и 5, эти звенья находятся в равновесии под действием двух сил. (для звена 5: F 65 = -F 56 = -F B5 = F 5B , а для звена 4: F 4B = -F B4 = -G 14 ).
(а) (б)
Когда у нас есть поршневой цилиндр, вместо того, чтобы рассматривать схемы свободного тела поршня и цилиндра по отдельности, удобнее нарисовать схему свободного тела двух звеньев (поршня и цилиндра) вместе, как показано на (а).Гидравлическое давление — это внутренняя сила, которая находится в равновесии, и единственная внешняя сила, действующая на систему, — это две совместные силы G 12 и F B3 (= — F 3B ), которые должны быть равными и противоположными ( G 12 = F 3B ), и их линия действия проходит вдоль линии, соединяющей точки приложения (A 0 B). Теперь уравнение равновесия сил F 3B + F 4B + F 5B = 0 может быть решено, так как направление сил F 3B , F 4B , а также величина и направление F 5B (= F 65 = -F 56 ) известны.Если ось ползуна между звеньями 2 и 3 совпадает с линией A 0 B, то в скользящем шарнире не будет силы соединения (т.е. F 23 = -F 32 = 0 и P = -F B3 ), как показано. Если поршневой цилиндр является эксцентричным, как показано на (b), то из диаграммы свободного тела поршневого цилиндра в целом можно определить линию действия G 12 и F B3 . Когда нарисована диаграмма свободного тела поршня, мы отмечаем, что здесь есть совместная сила F ‘ 23 и F’ 23 , действующая между звеньями 2 и 3.Обратите внимание, что даже если F 23 довольно мало, величины сил могут быть довольно большими (поэтому во всей строительной технике и т.п. у нас есть линейное расположение поршень-цилиндр. Смещенный поршень-цилиндр используется, если есть выбора нет.)
© es
границ | Вариации в управлении статической силой и поведении моторного блока с обратной связью с усилением ошибки у пожилых людей
Введение
Нарушение контроля устойчивости силы связано с небезопасными зрительно-моторными задачами у пожилых людей (Lodha et al., 2016). Что касается дегенеративных изменений нервно-мышечной системы, то выход силы у пожилых людей проявляется в большем размере (Vieluf et al., 2015) и регулярности (Vaillancourt and Newell, 2003; Sosnoff and Newell, 2008) в колебаниях силы. Связанное с возрастом увеличение колебаний силы указывает на нарушение точного контроля силы для создания силы (Temprado et al., 2017), отчасти потому, что длительная задержка в петле обратной связи мешает своевременному реагированию на отклонение слежения (Kennedy and Christou, 2011; Tracy et al., al., 2015). Увеличение регулярности силы с возрастом поддерживает потерю физиологической сложности в нейроповеденческой системе (Vaillancourt and Newell, 2003; Rey-Robert et al., 2011), что связано с неэффективностью использования визуальной информации для градации силы (Ofori et al., 2010). ). Поскольку колебания силы отражают механизм аддитивного контроля точности для исправления отклонений траектории (Slifkin et al., 2000), размерные изменения флуктуаций силы с возрастом связаны со снижением обнаружения ошибок с помощью процессов обратной связи и / или упреждающего воздействия (James and Kooy, 2011). ) в зависимости от условий окружающей среды (Morrison and Newell, 2015).С нейрофизиологического аспекта возрастное увеличение колебаний силы в первую очередь связано с увеличением вариабельности разряда двигательных единиц (Laidlaw et al., 1999; Tracy and Enoka, 2002; Tracy et al., 2005), лежащей в основе измененных свойств спинномоторного механизма. нейроны и большая вариабельность нисходящего драйва к мотонейронам (Hunter et al., 2016).
В нескольких недавних исследованиях утверждалось, что виртуальное отображение худших результатов или обратная связь с усилением ошибок (EA) обещает лучше оптимизировать зрительно-моторную задачу, чем фактическая обратная связь.Считается, что визуальный EA раздувает конфликты ответов и способствует сосредоточению внимания на двигательной задаче с помощью сетей мониторинга ошибок (Calhoun et al., 2002). Было показано, что обратная связь EA улучшает зрительно-моторные задачи точка-точка для здоровых пожилых людей (Bouchard et al., 2015) и неврологических пациентов (Abdollahi et al., 2014), а также позволяет выполнять задачу непрерывного статического отслеживания силы для молодых взрослые (Hwang et al., 2017). Для молодых людей во время статического изометрического сокращения зрительный ЭА может лучше стабилизировать выход силы с повышенной сложностью колебаний силы, что является следствием большего коэффициента вариации для интервалов между спайками и большей согласованности двигательных единиц на частоте 13–35 Гц (Hwang et al. ., 2017). Кроме того, EA производит стратегический сдвиг режима обратной связи и прямого распространения во время отслеживания синусоидальной силы (Chen et al., 2017). Visual EA подавлял фазовую разрядку двигательных единиц с помощью целевого сигнала в пользу использования процесса обратной связи для управления усилием рулевого управления. Однако мы не должны быть чрезмерно оптимистичными по отношению к ЭА, особенно когда пожилые люди постоянно выполняют зрительно-моторную задачу. Причина очевидна: пожилые люди могут быть не в состоянии использовать обширную пространственную информацию в визуальной обратной связи для оптимизации управления силой (Kennedy and Christou, 2011; Jordan et al., 2013; Park et al., 2017). Фактически, возрастные различия в вариабельности силы оказались минимальными при отсутствии визуальной обратной связи (Tracy et al., 2007). Нельзя отрицать, что ЭП может привести к информационной перегрузке пожилых людей, учитывая нарушение зрительно-моторной обработки. Кроме того, пожилые люди менее способны подавлять функционально нерелевантную информацию (шум), которая одновременно преувеличивается в процессе усиления (James and Kooy, 2011).
Поскольку влияние визуального EA на контроль силы у пожилых людей нельзя было исходить непосредственно из теоретической области, это исследование было направлено на изучение того, может ли обратная связь EA улучшить контроль силы низкоуровневого статического силового задания для здоровых пожилых участников в как поведенческие, так и нервные аспекты.В частности, мы определили сдвиги парадигмы в процессах обратной связи и прямой связи через динамику флуктуаций силы и охарактеризовали изменения в разряде моторных единиц с помощью технологии многоэлектродной поверхностной электромиографии (ЭМГ) и процедур разложения. Когда визуальная обратная связь состояла из быстрых изменений в информации об ошибках (таких как непроизвольные дрожащие движения), в отличие от молодых людей, была выдвинута гипотеза, что: (1) пожилые люди могут не получить пользу от EA для стабилизации силы из-за их относительной зависимости от дегенерированных система обратной связи; (2) пожилые люди могут демонстрировать увеличение вариабельности разряда и снижение сложности разряда двигательных единиц с высокочастотным ЭА; и (3) пожилые люди, использующие высокочастотную ЭА, могут демонстрировать снижение когерентности двигательных единиц на частоте 13–35 Гц, что важно для точного поддержания стабильного контроля силы.Наши выводы представляют ценность использования систем видеонаблюдения для тренировки зрительно-моторных навыков у пожилых людей.
Материалы и методы
Участников
Четырнадцать молодых людей (7 мужчин и 7 женщин; средний возраст: 24,9 ± 0,7 года) и 14 пожилых людей (6 мужчин и 8 женщин; средний возраст: 68,2 ± 1,0 года) вызвались участвовать в этом исследовании. Все участники были правши с нормальным или исправленным зрением, и ни у одного из них не было симптомов неврологических или нервно-мышечных заболеваний.Это исследование было одобрено институциональным наблюдательным советом (IRB) больницы Национального университета Ченг Кунг (NCKU), Тайвань. Все субъекты дали и подписали письменное информированное согласие в соответствии с Хельсинкской декларацией.
Экспериментальные процедуры
Участники выполнили задачи отслеживания силы в условиях обратной связи по ошибке с нормальным коэффициентом усиления (условие управления) и высоким коэффициентом усиления (условие улучшения ошибки). Каждое условие содержало три экспериментальных испытания, чередующихся с 3-минутными паузами, и все экспериментальные испытания выполнялись в рандомизированном порядке.Задачи на отслеживание силы требовали, чтобы участники сочетали статическую силу низкого уровня (20% от максимального произвольного сокращения (MVC)) с изометрическим индексом отведения на 27-дюймовом мониторе (пространственное разрешение: 1920 × 1080 пикселей). Перед экспериментом MVC первой дорсальной межкостной кости измеряли после трех 5-секундных попыток сокращения, разделенных 3-минутными паузами. Наивысшее значение силы каждого испытания было усреднено для получения MVC.
После 20-минутного периода отдыха во время теста MVC всем участникам было предложено по три практических испытания в каждом из условий обратной связи.Им было приказано создать изометрическую силу, прижав указательный палец к датчику силы (модель: MB-100, Interface Inc., Атланта, Джорджия, США), подключенному к индивидуальному усилителю (усиление = 10, частота среза). = 20 Гц). Пространственное разрешение (25 пикселей на 1% MVC) отображаемого целевого сигнала и выходной силы были идентичны для двух экспериментальных условий. Представление визуального разрешения было разработано, чтобы минимизировать влияние угла обзора и групповой разницы в силе на визуальную информацию (Kennedy and Christou, 2011).Участников проинструктировали достичь целевой силы в течение 2 секунд после латентного периода в 3 секунды, а затем поддерживать силу на уровне 20% от MVC в течение 34 секунд (Рисунок 1). На завершение экспериментального испытания ушло 44 с. Представляющим интерес временным окном была 7–37 секунда экспериментального испытания, в течение которого выходное усилие считалось относительно стабильным. Участники руководствовались предполагаемыми ошибками в условиях контроля и EA (Chen et al., 2017; Hwang et al., 2017). В состоянии EA вывод визуализированной силы (VF) был математически преобразован так, что размер визуализированной ошибки (VE) был фактически увеличен на 100% по сравнению с реальной ошибкой (RE) (VE = 2 * RE) (Рисунок 1 ).Использование коэффициента EA, равного двум, было эмпирически определено в лаборатории, потому что чрезмерный коэффициент EA может вызвать конфликты визуального восприятия и перегрузку визуальной информацией. В контрольных условиях участникам предоставляли RE (VE = RE). Однако участники этого исследования могли заметить больше ошибок выполнения высокочастотных компонентов, чем участники нашей предыдущей работы, которая не включала компоненты силы выше 6 Гц для расчета VE. Ожидалось, что включение в это исследование более высокочастотных компонентов (6–20 Гц) увеличит информационную нагрузку в состоянии EA.Выходная реальная сила (RF) была дискретизирована с частотой 1 кГц с помощью специальной программы на платформе LabVIEW (National Instruments Inc., Остин, Техас, США).
Рисунок 1 . Иллюстрация модуляции обратной связи увеличения ошибки. При математическом преобразовании VF выводит в состояние усиления ошибки (EA) фактически вдвое больше реальной ошибки выполнения, отображаемой в условии управления. В условиях контроля участнику была предоставлена реальная ошибка (VE = RE), так как выход VF был идентичен выходу RF.В состоянии EA выходное усилие, отображаемое на мониторе (VF), было преобразовано с VF = 2 * RF — T. Размер воспринимаемой ошибки отслеживания был увеличен в два раза в состоянии EA (VE = T — VF = T — (2 * RF — T) = 2 * (T — RF) = 2 * RE). Для данного экспериментального испытания самый правый график отображает VF примерно на 25-й секунде в условиях контроля (черная линия) и EA (синяя линия). VF, визуализированная сила; VE, визуализированная ошибка; РФ, действительная сила; RE, реальная ошибка; Т, целевой сигнал.
Электромиографические записи и разложение
Мышечная активность первой дорсальной межкостной кости регистрировалась с помощью многоэлектродной поверхностной ЭМГ-системы (система Bagnoli sEMG, Delsys Inc., Натик, Массачусетс, США). Аналоговые ЭМГ-сигналы от каждого пин-датчика усиливались (усиление = 1000) и фильтровались с полосой пропускания 20–450 Гц (De Luca et al., 2015a). Чтобы избежать перекоса фазы по каналам ЭМГ, использовалась высокая частота дискретизации 20 кГц (De Luca et al., 2006). Бинарные спайковые события разряда двигательных единиц, которые кодировали активации всех двигательных единиц со значениями 0 или 1, были охарактеризованы после разложения ЭМГ с использованием EMG works v.4.1 (Delsys Inc., Натик, Массачусетс, США), в соответствии с предыдущим доказательством. -of-Principle с использованием структуры искусственного интеллекта (De Luca et al., 2006; Nawab et al., 2010). Самые последние исследования неоднократно показывали, что алгоритм вычислений может давать убедительные результаты разложения, которые позволяют различать перекрывающиеся потенциалы действия для статического изометрического сокращения (Nawab et al., 2004; De Luca et al., 2015b) с помощью независимых методов проверки (Hu et al. , 2013). Достоверность разложения ЭМГ для каждой моторной единицы оценивалась с помощью теста «Разложение-синтез-разложение-сравнение» (De Luca et al., 1982, 2006), и моторные единицы с низкой точностью разложения (<90%) были отброшены.В предыдущих исследованиях сообщалось, что средняя точность разложения с использованием того же алгоритма колеблется от 92,5% до 97,6% (De Luca et al., 1982, 2006).
Анализ данных
Сигнал силы был обработан фильтром нижних частот (частота среза: 6 Гц). Результирующая сила была восприимчива к большинству зрительно-моторных процессов (Slifkin et al., 2000; Vaillancourt et al., 2002) и измерялась с понижением частоты дискретизации 100 Гц (рис. 1). С точки зрения% MVC, полная ошибка представляла собой среднеквадратичное значение рассогласования между целевым сигналом и выходным радиочастотным сигналом.Постоянная ошибка представляла собой разницу между усредненным выходным усилием и целевым сигналом. Величина колебаний силы была определена как среднеквадратичное значение выходного радиочастотного сигнала после удаления линейного тренда. Предполагалось, что флуктуации силы являются стационарными в широком смысле (инвариантное во времени среднее и автоковариация; Collins and De Luca, 1993), поэтому диффузионный анализ стабилограммы использовался для характеристики динамики флуктуаций силы степенным соотношением между средними значениями. -квадратное значение колебаний силы (<∆ F 2 >) и временного интервала (∆ t ), в котором эти значения произошли.Анализ диффузии стабилограммы может обнаруживать параметрические сдвиги регуляторов разомкнутого и замкнутого контура для системы позы из-за старения (Addamo et al., 2010; Toosizadeh et al., 2015) и изменения визуальной информации (Collins and De Luca, 1995 ). Анализ диффузии стабилограммы был рассчитан с использованием следующего уравнения: 〈ΔF2〉 = 〈[x (t + Δt) −x (t)] 2〉, где <●> обозначает среднее значение временного ряда. Вычисление ∆ F 2 было повторено с увеличением значений ∆ t в диапазоне от 0 до 5 с.График диффузии представлял собой среднеквадратичные колебания силы <∆ F 2 > в зависимости от временных интервалов ∆ t (рисунок 2A). Наклоны регрессии для краткосрочной и долгосрочной областей графика диффузии представляли собой два эффективных коэффициента диффузии (D s и D l ), которые описывали стохастическую активность механизмов управления силой с разомкнутым и замкнутым циклами. , соответственно. Критический момент времени (∆ t c ) был пересечением двух линий регрессии диффузионного графика, а вариации критической точки флуктуаций силы (<∆Fc2>) отражали сдвиг парадигмы между разомкнутым контуром и замкнутый цикл поведения (Collins and De Luca, 1993; Toosizadeh et al., 2015). Краткосрочные и долгосрочные показатели масштабирования (H s и H l ) были линейными аппроксимациями логарифмического графика диффузионного анализа стабилограммы (рис. 2B). Показатель масштабирования больше 0,5 указывает на то, что система управляется процессом без обратной связи и что ряды данных прошлого и будущего положительно коррелированы (Collins and De Luca, 1993, 1995). И наоборот, показатель масштабирования меньше 0,5 указывает на то, что ряды данных прошлого и будущего имеют отрицательную корреляцию, что регулируется процессом с обратной связью.
Рисунок 2 . Распространение сюжета. (A) Левый график представляет собой типичный линейно-линейный график диффузии. Обозначены вычисленная критическая точка (∆ t c , <∆Fc2>), кратковременный эффективный коэффициент диффузии (D s ) и долгосрочный эффективный коэффициент диффузии (D l ). Критическая точка указывает на поворотную точку изменения в разомкнутом и замкнутом управлении стохастической динамикой для флуктуаций силы.Средний и правый графики представляют собой объединенные линейно-линейные диффузионные графики молодых и пожилых людей. (B) Левый график представляет собой типичный логарифмический график диффузии. Обозначены вычисленный краткосрочный показатель масштабирования (H s ) и долгосрочный показатель масштабирования (H l ). Средний и правый графики представляют собой объединенные диаграммы диффузионного анализа молодых и пожилых людей.
Обработка разложения общих данных ЭМГ за 44 с использовалась для идентификации бинарных цепочек пиков, которые кодировали время разрядов двигательных единиц (рис. 3).Средний интервал между спайками двигательной единицы представлял собой усредненные временные интервалы последовательности спайков двигательной единицы в интересующем временном окне, а общее среднее значение среднего ISI (ISI GAV ) было средним средним интервалом между спайками для все двигательные агрегаты. Вариабельность интервала между спайками для отдельной двигательной единицы характеризовалась коэффициентом вариации (ISI CV). Среднее значение ISI CV (ISI CV GAV ) было средним значением ISI CV всех моторных единиц.Поскольку силовое поведение настроено на совокупную разрядку двигательных единиц, мы оценили кумулятивную скорость разрядки путем свертки кумулятивных последовательностей импульсов всех идентифицируемых двигательных единиц с окном Хеннинга длительностью 400 мс (рис. 3). Результирующая низкочастотная кумулятивная скорость разряда отражает эффективное нервное воздействие на мышцу, а динамика колебаний силы может в значительной степени характеризоваться суммарной скоростью разряда во время статического изометрического сокращения (Negro and Farina, 2012; Farina et al., 2016).Размер и сложность кумулятивной изменчивости скорости разряда были определены с помощью RMS и многомасштабной энтропии (MSE) после процесса понижающей дискретизации при 100 Гц и удаления его линейного тренда. MSE учитывает сложность сигналов в различных временных масштабах, предложенная Коста и др. (2005). Основываясь на выборочной энтропии, этот метод количественно определяет регулярность временного ряда с помощью нескольких крупнозернистых временных рядов с помощью масштабного коэффициента τ . Для одномерного временного ряда совокупной скорости разряда { x i … x n } MSE сначала строит несколько крупнозернистых временных рядов с масштабным коэффициентом τ .yj (τ) = 1 / τ∑i = (j − 1) τ + 1jτxi, 1≤j≤N / τ. N — количество точек данных во временном ряду. Для первого масштаба временной ряд { y (1) } — это просто исходный временной ряд. Длина каждого крупномасштабного временного ряда равна длине исходного временного ряда, деленной на масштабный коэффициент τ . Затем энтропия образца была применена к результирующему крупнозернистому временному ряду, построенному как функция масштабного коэффициента τ или кривой MSE. Сложность совокупной скорости сброса была обозначена как области (MSE 1–10 и MSE 11–20 ) под кривой MSE для короткого (1–10) и длительного (11–20) временных масштабов.Каждый временной масштаб составлял 10 мс в соответствии с частотой понижающей дискретизации. Математическая формула энтропии образца была SampEn (m, r, N) = — log (∑i = 1N − mAi∑i = 1N − mBi), где r = 15% стандартного отклонения силового канала, м — длина шаблона ( м = 2), а A i — количество совпадений i -го шаблона длиной м + 1 точек данных, и B i — количество совпадений i -го шаблона длиной м точек данных. N представляет собой количество точек данных временного ряда (Pethick et al., 2015). Меньшее значение означает большую регулярность силовых характеристик. Кроме того, мы рассчитали единый спектр когерентности между данной парой кумулятивных цепочек спайков из пяти цепочек спайков моторных единиц (Rosenbaum et al., 2011; Farina et al., 2016). Вычисления объединенной когерентности двигательных единиц были повторены и усреднены по 500 случайным комбинациям единого спектра когерентности от всех идентифицируемых двигательных единиц.Квадраты значений когерентности (C) были оценены с помощью двух нефильтрованных составных последовательностей спайков с использованием окна Хеннинга 1 с и перекрытия 90% (Castronovo et al., 2015). Значения когерентности были преобразованы в значения Z (FZ) Фишера (Amjad et al., 1997), чтобы минимизировать внутреннее смещение оценок когерентности из каждого профиля сегмента после корректирующего вычитания средней когерентности между 100 Гц и 500 Гц (Castronovo et al. ., 2015). Значение FZ формулируется как: FZ = tan − 1 (C). После преобразования z мы вычли среднюю когерентность между 100 Гц и 500 Гц из каждого профиля когерентности, потому что средняя когерентность не содержала значительной когерентности (Witte et al., 2007; Nawab et al., 2010). Объединенная когерентность моторных единиц, которая отражает общее стремление к пулу мотонейронов в спектральной области, содержала два заметных спектральных пика в диапазоне 0–4 Гц (ZC 0–4 Гц ) и 13–35 Гц (ZC 13 –35 Гц ; Hwang et al., 2017). Все силовые переменные и переменные разряда трех экспериментальных испытаний в условиях контроля и EA были рассчитаны и усреднены для каждого субъекта. Обработка сигналов и статистический анализ были выполнены с использованием Matlab (Mathworks Inc., Натик, Массачусетс, США).
Рисунок 3 . Выделение признака совокупной скорости сброса. Кумулятивная скорость разряда — это сумма всех шиповых составов моторных агрегатов после процесса сглаживания и удаления линейного тренда. Размер и сложность совокупной скорости разряда представлены с помощью среднеквадратичного значения (RMS) и многомасштабной энтропии (MSE).
Статистический анализ
Значения MVC индекса абдукции молодых и старших групп сравнивались с независимой статистикой t .При соответствующем преобразовании переменных, чтобы удовлетворить двухсторонний дисперсионный анализ с повторными измерениями (ANOVA), был использован для изучения эффекта задачи (контроль против EA, внутрисубъектный фактор) и группового эффекта (молодой против старшего, межсубъектный фактор) от переменных колебаний задачи / силы, переменных анализа диффузии стабилограммы и переменных расхода моторных единиц. Уровень значимости 0,05. Post hoc тестирование проводилось при наличии значительного взаимодействия или основных эффектов.Особый интерес в этом исследовании вызвала дифференциальная модуляция поведения силы и двигательных единиц между молодыми и пожилыми людьми из-за ЭА. Поправки Бонферрони использовались для определения альфа-уровня значимости для апостериорных тестов ( p = 0,0125). Данные представлены как средние по группе ± 1 стандартная ошибка среднего. Все статистические анализы были выполнены в IBM SPSS Statistics (v19).
Результаты
Ошибка задания и характеристики силы
В таблице 1 приведены сводные результаты переменных производительности для молодых и пожилых людей.Постоянная ошибка не зависела ни от задачи, ни от групповых эффектов ( p > 0,05). Напротив, общая ошибка отслеживания силы зависела от задач и групповых эффектов ( p <0,05) со значительным взаимодействием задача × группа ( p = 0,013). Post hoc анализ показал, что только старшая группа показала большую общую ошибку в состоянии EA, чем в контрольном состоянии ( p = 0,002). Кроме того, общая ошибка старшей группы была больше, чем у молодой группы в EA ( p <0.001) состояние. Размер колебаний силы также зависел как от задачи, так и от групповых эффектов ( p <0,05) со значительным взаимодействием задача × группа ( p = 0,019). Post hoc анализ показал, что только старшая группа показала больший размер колебаний силы в состоянии EA, чем в контрольном состоянии ( p <0,001). Величина силовых колебаний старшей группы была больше, чем у молодой группы в EA ( p = 0.001) состояние.
Таблица 1 . Результаты статистического анализа дисперсии (ANOVA) для сравнения переменных производительности между молодой и старой группами в условиях контроля и EA.
Объединенные линейно-линейные и логарифмические графики диффузионного анализа стабилограммы показаны на рисунках 2A, B, соответственно. В таблице 2 приведены результаты статистики дисперсионного анализа для всех переменных диффузионного анализа стабилограммы. ∆ t c значительно варьировалось при изменении коэффициента ошибки ( p = 0.001), а ∆ t c из более старых ( p = 0,008) групп была меньше в состоянии EA, чем в контрольном состоянии. <ΔFc2> и D s подвергались значительному эффекту взаимодействия задача × группа ( p <0,05). Post hoc анализ далее показал, что <ΔFc2> и D s модулировались по-разному для двух групп. <ΔFc2> и D s были больше в состоянии EA, чем в контрольном состоянии, только для пожилых людей (<ΔFc2>: p = 0.004; D с : p = 0,001). H s был функцией эффекта задачи ( p = 0,005), а тест post hoc показал, что EA улучшил H s для старшей группы ( p = 0,002). Ни один из <ΔFc2>, D s и H s молодых людей не зависел от манипуляции EA ( p > 0,05). Кроме того, D l и H l не менялись с основными эффектами и эффектами взаимодействия задачи и группы ( p > 0.05).
Таблица 2 . Параметры диффузионного анализа стабилограммы слежения за статической силой для молодых и старых групп в контроле и условиях ЭО.
Схема разряда моторных агрегатов
Среднее количество разложившихся двигательных единиц у пожилых людей в контрольных условиях и в условиях EA составляло 26,7 ± 1,1 и 28,0 ± 1,4 соответственно. Среднее количество разложившихся двигательных единиц у молодых людей в контрольных условиях и в условиях ЭА составляло 27,0 ± 1,0 и 27.4 ± 1,2 соответственно. В таблице 3 показаны статистические результаты ANOVA для переменных расхода моторных единиц. И ISI GAV , и ISI CV GAV были подвержены незначительно значимому эффекту взаимодействия задачи × группы (ISI GAV : p = 0,058; ISI CV GAV : p = 0,050). Для благоразумия, ретроспективный анализ показал, что только переменные разряда пожилых людей зависели от эффекта задачи, со значительно большим ISI GAV ( p = 0.005) и ISI CV GAV ( p = 0,007) в состоянии EA, чем в состоянии управления. Переменные разрядки молодых людей были нечувствительны к эффекту задания ( p > 0,05). ISI CV GAV пожилых людей был больше, чем ISI CV GAV молодых людей в состоянии EA ( p = 0,005).
Таблица 3 . Средние и стандартные ошибки переменных разряда для молодых и старых групп в условиях контроля и EA.
На рис. 3 показан типичный пример совокупной частоты выписки из исследования ЭА у пожилого взрослого. Контрасты размера и сложности кумулятивной изменчивости скорости разряда между молодыми и пожилыми людьми в контрольных условиях и в условиях EA показаны на рисунках 4A – C. С точки зрения среднеквадратичного значения, среднеквадратичное значение совокупной скорости разряда было предметом задачи ( F (1,26) = 4,95, p = 0,035, η 2 = 0,163) и группы ( F (1,26) = 5.93, p = 0,022, η 2 = 0,058) эффекты со значительным эффектом взаимодействия группы и задачи ( F (1,26) = 5,61, p = 0,026, η 2 = 0,066). Post hoc анализ показал, что RMS кумулятивной скорости выпадения была выше в состоянии EA, чем в контрольном состоянии для пожилых людей ( p = 0,003), тогда как тенденция не была очевидной для молодого взрослого ( p = 0.920). Групповой эффект был отмечен в состоянии EA, и RMS кумулятивной скорости выписки у пожилых людей был больше, чем у молодых людей ( p = 0,002). На рисунке 4B показаны объединенные кривые MSE для молодых и пожилых людей, которые представляют сложность кумулятивной изменчивости скорости разряда в различных временных масштабах в условиях контроля и EA. Кратковременная шкала MSE (MSE 1–10 ) подвергалась группе ( F (1,26) = 4,84, p = 0.037, η 2 = 0,140) и задача ( F (1,26) = 6,29, p = 0,019, η 2 = 0,098; рисунок 4C). Только MSE 1–10 пожилых людей подавлялась с помощью EA ( p = 0,010), а не MSE 1–10 молодых людей ( p = 0,459). В состоянии EA MSE 1–10 пожилых людей была меньше, чем у молодых людей ( p = 0,011). Долгосрочная шкала MSE (MSE 11–20 ) подверглась значительному влиянию задачи ( F (1,26) = 5.58, p = 0,023, η 2 = 0,086) и незначительно значимый эффект взаимодействия задачи и группы ( F (1,26) = 2,99, p = 0,056, η 2 = 0,069), а не групповой эффект ( F (1,26) = 2,04, p = 0,165, η 2 = 0,027). Post hoc анализ далее показал, что MSE 11–20 старшей группы была ниже в состоянии EA, чем в контрольном состоянии ( p = 0.011). MSE 11–20 молодой группы не зависела от EA ( p = 0,487).
Рисунок 4 . Средние значения совокупности и стандартные ошибки для параметрических переменных совокупной скорости сброса в условиях контроля и EA. (A) RMS; (B) MSE; (C) MSE область низких (1–10) и высоких (11–20) масштабов времени. Каждый временной масштаб кривой MSE составляет 10 мс, что соответствует частоте понижающей дискретизации 100 Гц.
На рис. 5A сравнивается совокупная согласованность двигательных единиц между контролем и условиями EA для молодых и пожилых людей.Объединенная когерентность двигательных единиц пожилых людей была более изменяема ЭА во время отслеживания силы. Групповой эффект ZC 13–35 Гц был значимым ( F (1,26) = 6,25, p = 0,019, η 2 = 0,053) с незначительно значимым взаимодействием задачи × групповое взаимодействие ( F (1,26) = 10,12, p = 0,056, η 2 = 0,034) и незначительный групповой эффект ( F (1,26) = 1.11, p = 0,310, η 2 = 0,037). Только ZC 13–35 Гц из старшей группы был значительно подавлен ЭА ( p = 0,004), но не у молодых людей ( p > 0,05; Рисунок 5B). Однако ZC 0–4 Гц не изменялся в зависимости от основных и взаимосвязанных эффектов возраста и размера ошибки ( p > 0,05).
Рисунок 5 . Согласованность разряда между двигательными единицами. (A) Контраст согласованности объединенных двигательных единиц между контролем и условиями EA для молодых и старых групп. (B) Контраст средних и стандартных ошибок пиков когерентности в диапазонах 0–4 Гц (ZC 0–4 Гц ) и 13–35 Гц (ZC 13–35 Гц ) между контрольной и Условия EA для двух групп.
Обсуждение
Новым открытием этого исследования стало различное возрастное влияние визуального EA на статическое отслеживание силы с визуальной обратной связью, содержащей информацию об ошибках с более высокой частотой. Высокочастотный визуальный советник изменил стратегический баланс между элементами управления с разомкнутым и замкнутым контуром, чтобы управлять статическим отслеживанием силы.Однако, в отличие от молодых людей, пожилые люди демонстрировали более низкую точность выполнения задания, большую вариабельность разряда моторных единиц, меньшую сложность вариабельности разряда и более низкую совокупную когерентность моторных единиц в диапазоне 13–35 Гц в состоянии EA, чем в контрольном состоянии. Напротив, статическое отслеживание силы у молодых людей в меньшей степени зависело от высокочастотного зрительного ЭА в поведенческом и нейрофизиологическом аспектах.
Возрастное повышение точности задания с увеличением погрешности
Было ясно, что высокочастотный ЭА оказывает негативное влияние на пожилых людей, которые показали меньшую точность выполнения задания с увеличением общей ошибки в состоянии ЭА (Таблица 1).Напротив, молодые люди гораздо меньше пострадали от ЭА. Эффект возраста оказал различное влияние на точность выполнения задания с EA, что в первую очередь связано с величиной колебаний силы, а не с постоянной ошибкой (Таблица 1). Хотя пожилые люди стали неспособны поддерживать постоянство силы с помощью EA во время отслеживания силы, степень линейных сдвигов силы от целевого сигнала, которая была значительно снижена для пожилых людей с увеличенным пространственным разрешением для представления силы на мониторе, была независимой. эффекта возраста и EA (Sosnoff, Newell, 2006; Kennedy, Christou, 2011).Следовательно, возрастное снижение устойчивости силы с EA в этом исследовании не было точно связано с чрезмерной визуально-пространственной информацией (Kennedy and Christou, 2011; Tracy et al., 2015), поскольку пространственное разрешение монитора для контроля и EA условия были идентичны. Вместо этого мы указали, что нарушение устойчивости силы, индуцированной EA, у пожилых людей было следствием возрастного увеличения задержки зрительно-моторной петли, особенно когда управление отслеживанием силы с EA основывалось на процессе обратной связи (Chen et al. ., 2017). Воспринимаемые ошибки (или виртуально усиленные ошибки) легче накапливались с течением времени в системе обратной связи, что приводило к колебаниям выходной силы у более старших участников (Miall et al., 1986, 1993). Свидетельство переключения схемы во время EA дополнительно обсуждается в следующем разделе.
Усиление визуальных ошибок и процесс, подверженный обратной связи
Относительная значимость зрительно-моторного контроля моделируется непрерывным режимом от обратной связи до прямой связи, в зависимости от условий окружающей среды (Slifkin et al., 2000). Переключение схемы управления статической силой было исследовано с помощью диффузионного анализа стабилограммы, концептуально аналогичного показателю Херста. Поскольку динамику флуктуаций силы можно смоделировать с помощью двух линий линейной регрессии на диффузионном графике стабилограммы, система флуктуаций силы должна регулироваться двумя отдельными процессами (процессами прямой связи и обратной связи) параллельно с системой контроля положения тела (Collins and De Luca, 1993). ; Amoud et al., 2007). В этом исследовании краткосрочный показатель масштабирования (H s ) находился в диапазоне 0.5–1. Система краткосрочных колебаний силы была постоянной и подвергалась процессу прямой связи, так что за высоким значением колебаний силы следовало другое высокое значение колебаний силы. Напротив, долгосрочный показатель масштабирования (H l ) был меньше 0,5. Долговременные колебания силы в прошлом и будущем имели отрицательную корреляцию, в которой преобладала отрицательная обратная связь.
Значительное влияние задачи EA на критическую точку времени (∆ t c ) и критическую точку колебания силы <ΔFc2> (Таблица 2) подразумевает изменение поведения стационарных колебаний силы из-за EA.Известно, что ∆ t c отражает время стохастической активности, когда колебания силы имеют тенденцию дрейфовать от точки равновесия в режиме управления без обратной связи до того, как механизмы обратной связи с обратной связью доминируют в поведении колебаний силы. Таким образом, уменьшение ∆ t c в состоянии EA показало, что эффективный диапазон интервала (0-∆ t c ) для регулирования колебаний силы в режиме разомкнутого контура был сокращен.Одновременно в состоянии EA увеличился эффективный диапазон интервала (> ∆ t c ), в течение которого стохастическая активность флуктуаций силы показала отрицательную корреляцию между своим приращением (анти-персистентностью) из-за процесса обратной связи. Более высокая зависимость от механизма обратной связи для стабилизации статической силы в состоянии EA хорошо совместима с нашей предыдущей работой по отслеживанию ритмической силы (Chen et al., 2017). Следует отметить, что в отличие от молодых людей, у которых наблюдалась тенденция к снижению <ΔFc2> в состоянии EA, у пожилых людей наблюдалось связанное с EA потенцирование критической точки колебания силы (<ΔFc2>; Таблица 2).Сценарий предполагает, что обратная связь с обратной связью пожилых людей в состоянии EA была задействована, когда размер колебания силы был больше, чем в условиях контроля. Отсроченный процесс обратной связи может связываться с дегенерированными сенсорными системами, чтобы разумно обнаруживать ошибки силы у пожилых людей. Фактически, стратегия обременения сенсорной обратной связи с помощью ЭА не подходила для пожилых людей, потому что их дегенерированные сенсорные системы также могли преувеличивать неоднозначность обратной связи и сенсорные конфликты (Bates and Wolbers, 2014).
Согласно принципу стохастического резонанса (Moss et al., 2004), шум не всегда отрицателен для управляемого процесса. Добавление соответствующего количества шумов может быть полезным для восприятия сенсорных сигналов, которые невозможно обнаружить (подпороговая сенсорная информация; Moss et al., 2004; McDonnell and Abbott, 2009). Тем не менее, это исследование не касалось преимуществ шума. Все участники этого исследования смогли четко обнаружить ошибки выполнения на мониторе, а добавление случайных шумов могло просто вызвать неопределенность в зрительно-моторном контроле.Фактически, влияние неопределенности из-за шумных визуальных ошибок следует минимизировать с помощью процесса фильтрации. Например, если информация об ошибке содержала высокочастотные дрожащие движения (такие как физиологический тремор с частотой 8–12 Гц), которые были увеличены с помощью процесса EA, информация об ошибке выше 0,4 Гц вряд ли может быть обработана механизмом обратной связи из-за зрительно-моторной задержки (50– 300 мс для людей; Миалл и др., 1986, 1993; Джойнер и Шелхамер, 2009). Более того, согласно гипотезе тормозящего дефицита, пожилые люди могут не игнорировать функционально нерелевантные зрительные стимулы, такие как высокочастотные ошибки (Van Gerven and Guerreiro, 2016).А именно, зашумленная обратная связь по ошибке мешала корректировке отслеживания отклонений. Более того, наблюдение, что EA увеличило краткосрочные эффективные коэффициенты диффузии (D s ) и показатель масштабирования (H s ), было отмечено только у пожилых людей (Таблица 2). Хотя было неясно, почему у пожилых людей наблюдалась более высокая положительная корреляция между прошлыми и будущими данными о колебаниях силы за короткий промежуток времени, исследователи, которые использовали диффузионный анализ стабилограммы для исследования постуральной регуляции, приписывают параметрические изменения увеличению жесткости в голеностопном суставе. с совместной активностью антагонистов при компенсации мышечной слабости (Collins and De Luca, 1995; Toosizadeh et al., 2015).
Возрастные вариации в поведении разряда из-за увеличения погрешности
В целом, только поведение при выписке и совокупная частота выпадения пожилых людей были настроены на ЭА; у молодых людей не было. У пожилых людей высокочастотная ЭА добавлялась к вариабельности разряда двигательных единиц и интервала между спайками (Таблица 3). Сообщается, что разряд двигательных единиц у пожилых людей более восприимчив к объему зрительно-пространственной информации во время зрительно-моторной задачи (Vaillancourt et al., 2002; Jordan et al., 2013). В соответствии с этой интерпретацией, высокочастотный EA для пожилых людей, по-видимому, вызывал более вариативные синаптические сигналы (нейронные шумы) мотонейронам для зрительно-моторной коррекции. Этот аргумент также подтверждается возрастным увеличением RMS совокупной скорости выпадения пожилых людей в состоянии EA (рис. 4A). С другой стороны, сложность вариативности разряда была по-разному организована в зависимости от возраста и задачи. Более низкая краткосрочная шкала MSE 1–10 для пожилых людей (рисунки 4B, C) объединяет гипотезу потери сложности со старением, хотя ни одно из предыдущих исследований не выявило этот факт на основе комплексных измерений вариабельности разряда двигательных единиц (Rey -Роберт и др., 2011; Моррисон и Ньюэлл, 2015). Для пожилых людей было очевидно, что высокочастотная ЭА вызывает аномалии во временной организации динамики разряда двигательных единиц ввиду более низкой кратковременной MSE 1–10 и продолжительной MSE 11–20 в состоянии EA, чем в состоянии управления. Этот сценарий предполагает снижение способности по мере старения использовать более быстрые временные шкалы визуальной информации (Sosnoff and Newell, 2008). Когда размер ошибки в визуальной обратной связи был увеличен, пожилые люди не смогли сохранить стабильность и гибкость разряда двигательных единиц перед ограничением задачи, потому что преувеличенная информация об ошибках поставила под сомнение внутреннюю надежность компонентов мозга, которые менее способны компенсировать повышенный шум обработки большими время задержки обратной связи для пожилых людей (Heenan et al., 2014). Следует отметить, что серьезное снижение сложности выполнения разгрузочной вариабельности двигательных единиц для молодой группы было далеко не очевидным. Этот аргумент подтверждается связанным с EA сокращением общих колебательных входов в диапазоне 13–35 Гц для старшей группы (Рисунки 5A, B). Когерентность моторных единиц β-диапазона отражает взаимодействие между кортикальными и спинномозговыми цепями, и ее величина варьируется в зависимости от требований сенсомоторной интеграции. Было показано, что когерентность моторных единиц β-диапазона увеличивается пропорционально увеличению количества зрительно-пространственных данных (Laine et al., 2014) и информация об ошибках (Hwang et al., 2017) для молодых людей во время задачи по отслеживанию сил. По совпадению, повышенная когерентность электроэнцефалографии (ЭЭГ) β-диапазона связана с устойчивым контролем силы с более высокой степенью фокуса внимания (Kristeva et al., 2007; Witte et al., 2007). Если когерентность двигательных единиц β-диапазона является следствием ЭМГ-ЭЭГ β-диапазона, снижение согласованности двигательных единиц β-диапазона с EA означает, что пожилые люди были отвлечены от выполнения конструктивной настройки силы.Кроме того, мы не могли исключить возможность того, что зависящие от возраста вариации разряда двигательных единиц были физиологическим следствием увеличения совместной активности антагонистов, поскольку пожилые люди производят больший моторный переток антагонистов во время когнитивно сложной задачи, чем молодые. взрослые (Addamo et al., 2010). Было рационально наблюдать более длительный ISI, большую вариабельность разряда и увеличение D s и показателей масштабирования с EA для пожилых людей.
Методологические соображения
Во-первых, предполагается, что EA является эффективным способом оптимизации отслеживания статической силы для молодых людей (Hwang et al., 2017). Однако ожидаемые функциональные преимущества не были очевидны для молодых людей, потому что мы ввели высокочастотные компоненты силы (частота среза: 20 Гц против 6 Гц, в этом исследовании и в предыдущем исследовании, соответственно) и больший коэффициент EA. (2 против 1,5, в этом исследовании и в предыдущем исследовании, соответственно), чтобы определить размер обратной связи об ошибке. Следовательно, функциональные достоинства EA для молодых людей были частично уравновешены увеличением шумной обратной связи и чрезмерным фактором EA.Ньют, одно из методологических преимуществ использования разложения поверхностной ЭМГ заключается в том, что он может обнаруживать больше активных двигательных единиц, чем внутримышечная ЭМГ. Разложение поверхностной ЭМГ было принято во многих исследованиях (De Luca et al., 2006; Hu et al., 2014; Martinez-Valdes et al., 2016; Chen et al., 2017; Hwang et al., 2017), хотя Точность разложения среди различных алгоритмов остается спорной (Farina and Enoka, 2011; De Luca et al., 2015b). Решение вопросов точности разложения выходит за рамки данного исследования.
В заключение, визуальный EA, содержащий высокочастотную информацию об ошибках, ухудшает контроль статической силы у пожилых людей из-за неэффективной обработки информации с помощью замкнутой системы. Использование визуального ЭА усиливает нервные шумы в свете увеличения вариабельности разряда двигательных единиц. По сравнению с контрольным условием, кумулятивная скорость разряда пожилых людей при ЭА более вариативна и менее сложна, параллельно с поведенческими изменениями прижимной силы.В совокупности изменения в разряде двигательных единиц из-за увеличения виртуального размера высокочастотной информации об ошибках связаны с уменьшением общего возбуждения мотонейронального пула для стабилизации силы.
Авторские взносы
Y-CC и I-SH: концепция или дизайн работы. LLL, C-LH: приобретение. I-SH, Y-TL, Y-CC: анализ. Y-CC, I-SH, LLL: интерпретация данных. I-SH и Y-CC: составление проекта работы или ее критический пересмотр на предмет важного интеллектуального содержания.I-SH: окончательное утверждение версии, которая будет опубликована. Y-CC и I-SH: согласие нести ответственность за все аспекты работы, обеспечивая надлежащее расследование и решение вопросов, связанных с точностью или целостностью любой части работы.
Финансирование
Это исследование было поддержано грантами Министерства науки и технологий Тайваня, Р.О.К., под номерами грантов MOST 105-2410-H-040-009 и MOST 104-2314-B-006-016-MY3.
Заявление о конфликте интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могут быть истолкованы как потенциальный конфликт интересов.
Сокращения
∆ t c , критический момент времени; <∆ F 2 > — среднеквадратичное значение колебаний силы; <ΔFc2> — критическая точка колебаний силы; D s , кратковременный эффективный коэффициент диффузии; D l , длительный эффективный коэффициент диффузии; ЭЭГ, электроэнцефалография; ЭМГ, электромиография; FZ — значение Z Фишера; H s , кратковременный масштабный показатель; H l , долгосрочный масштабный показатель; ISI GAV , среднее значение среднего интервала между спайками; ISI CV GAV , общее среднее для коэффициента вариации интервала между спайками; MSE, многомасштабная энтропия; MVC — максимальное произвольное сокращение; RE, реальная ошибка; РФ, действительная сила; RMS, среднеквадратичное значение; Т — целевой сигнал; VE, визуализированная ошибка; VF, визуализированная сила; ZC 0–4 Гц, пик когерентности двигательных единиц в диапазоне 0–4 Гц; ZC 13–35 Гц, пик когерентности моторного блока в диапазоне 13–35 Гц
Список литературы
Абдоллахи, Ф., Case Lazarro, E. D., Listenberger, M., Kenyon, R. V., Kovic, M., Bogey, R.A., et al. (2014). Увеличение ошибок, улучшающее восстановление руки у лиц с хроническим инсультом: рандомизированный перекрестный дизайн. Neurorehabil. Ремонт нейронов 28, 120–128. DOI: 10.1177 / 1545968313498649
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Аддамо П. К., Фэрроу М., Брэдшоу Дж. Л., Мосс С. и Георгиу-Каристианис Н. (2010). Влияние внимания к моторному переполнению на его произвольное торможение у молодых и пожилых людей. Brain Cogn. 74, 358–364. DOI: 10.1016 / j.bandc.2010.10.001
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Амджад, А. М., Холлидей, Д. М., Розенберг, Дж. Р., и Конвей, Б. А. (1997). Расширенный тест на различие когерентности для сравнения и объединения нескольких независимых оценок когерентности: теория и применение к изучению двигательных единиц и физиологического тремора. J. Neurosci. Методы 73, 69–79. DOI: 10.1016 / s0165-0270 (96) 02214-5
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Амуд, Х., Абади, М., Хьюсон, Д. Дж., Мишель-Пеллегрино, В., Дуссо, М., и Дюшен, Дж. (2007). Фрактальный анализ временных рядов устойчивости позы у пожилых людей и субъектов контрольной группы. J. Neuroeng. Rehabil. 4:12. DOI: 10.1186 / 1743-0003-4-12
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Бейтс, С. Л., и Вольберс, Т. (2014). Как когнитивное старение влияет на мультисенсорную интеграцию навигационных сигналов. Neurobiol. Старение 35, 2761–2769. DOI: 10.1016 / j. neurobiolaging.2014.04.003
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Бушар, А. Э., Корриво, Х., Милот, М. Х. (2015). Сравнение тактильного наведения и роботизированных тренировок с усилением ошибок для изучения двигательной задачи на основе времени здоровыми пожилыми людьми. Фронт. Syst. Neurosci. 9:52. DOI: 10.3389 / fnsys.2015.00052
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Калхун, В. Д., Пекар, Дж. Дж., МакГинти, В. Б., Адали, Т., Уотсон, Т.Д., и Перлсон, Г.Д. (2002). Различная динамика активации в нескольких нейронных системах во время имитации вождения. Hum. Brain Mapp. 16, 158–167. DOI: 10.1002 / hbm.10032
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Кастроново, А. М., Негро, Ф., Конфорто, С., и Фарина, Д. (2015). Доля общего синаптического входа в двигательные нейроны увеличивается с увеличением чистого возбуждающего входа. J. Appl. Physiol. 119, 1337–1346.DOI: 10.1152 / japplphysiol.00255.2015
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Чен, Ю. К., Лин, Ю. Т., Чанг, Г. К., и Хван, И. С. (2017). Парадигма меняется в произвольном контроле силы и поведении двигательных единиц с изменяемым размером визуального восприятия ошибок. Фронт. Physiol. 8: 140. DOI: 10.3389 / fphys.2017.00140
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Коллинз, Дж. Дж., И Де Лука, К. Дж. (1993).Разомкнутый и замкнутый контроль позы: анализ случайного блуждания траекторий центра давления. Exp. Brain Res. 95, 308–318. DOI: 10.1007 / bf00229788
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Коллинз, Дж. Дж., И Де Лука, К. Дж. (1995). Влияние визуального ввода на механизмы контроля позы с разомкнутым и замкнутым контуром. Exp. Brain Res. 103, 151–163. DOI: 10.1007 / bf00241972
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Коста, М., Голдбергер, А. Л., и Пэн, К. К. (2005). Многомасштабный энтропийный анализ биологических сигналов. Phys. Rev. E Stat. Нелин. Soft Matter Phys. 71: 021906. DOI: 10.1103 / PhysRevE.71.021906
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Де Лука, К. Дж., Адам, А., Вотиз, Р., Гилмор, Л. Д., и Наваб, С. Х. (2006). Разложение сигналов поверхностной ЭМГ. J. Neurophysiol. 96, 1646–1657. DOI: 10.1152 / jn.00009.2006
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Де Лука, К.Дж., Чанг, С. С., Рой, С. Х., Клайн, Дж. К., и Наваб, С. Х. (2015a). Разложение сигналов поверхностной ЭМГ от циклических динамических сокращений. J. Neurophysiol. 113, 1941–1951. DOI: 10.1152 / jn.00555.2014
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Де Лука, К. Дж., Наваб, С. Х., Клайн, Дж. К. (2015b). Уточнение методов, используемых для проверки алгоритмов разложения поверхностной ЭМГ, как описано Farina et al. (2014). J. Appl. Physiol. 118: 1084.DOI: 10.1152 / japplphysiol.00061.2015
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Де Лука, К. Дж., ЛеФевер, Р. С., МакКью, М. П., и Ксенакис, А. П. (1982). Схема управления одновременно активными двигательными единицами человека во время произвольных сокращений. J. Physiol. 329, 129–142. DOI: 10.1113 / jphysiol.1982.sp014294
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Фарина Д., Негро Ф., Муцели С. и Енока Р. М.(2016). Принципы физиологии двигательных единиц развиваются с развитием технологий. Physiology (Bethesda) 31, 83–94. DOI: 10.1152 / Physiol.00040.2015
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Хинан М., Шайдт Р. А. и Бердсли С. А. (2014). Возрастная дифференциация стратегий сенсомоторного контроля при преследовании и компенсаторном отслеживании. конф. Proc. IEEE Eng. Med. Bio.l Soc 2014, 3562–3565. DOI: 10.1109 / embc.2014.6944392
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Ху, Х., Раймер, В. З., Суреш, Н. Л. (2013). Оценка достоверности разложения высокопрочной поверхностной электромиограммы. J. Neuroeng. Rehabil. 10:99. DOI: 10.1186 / 1743-0003-10-99
CrossRef Полный текст | Google Scholar
Ху X., Раймер В. З., Суреш Н. Л. (2014). Оценка точности системы разложения поверхностной электромиограммы первой спинной межкостной мышцы человека. J. Neural Eng. 11: 026007. DOI: 10.1088 / 1741-2560 / 11/2/026007
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Хантер, С.К., Перейра, Х. М., и Кинан, К. Г. (2016). Старение нервно-мышечной системы и двигательная активность. J. Appl. Physiol. 121, 982–995. DOI: 10.1152 / japplphysiol.00475.2016
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Хван И.С., Линь Ю.Т., Хуанг В.М., Ян З.Р., Ху К.Л. и Чен Ю.С. (2017). Изменения в нейронном контроле постоянного изометрического сжатия с размером ошибки обратной связи. PLoS One 12: e0170824. DOI: 10,1371 / журнал.pone.0170824
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Джойнер, В. М., и Шелхамер, М. (2009). Модель оценки времени и обратной связи по ошибкам в прогнозирующем временном поведении. J. Comput. Neurosci. 26, 119–138. DOI: 10.1007 / s10827-008-0102-x
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Джордан, К., Джесунатадас, М., Сарчет, Д. М., и Энока, Р. М. (2013). Долгосрочные корреляции времени разряда моторных единиц при малых усилиях модулируются усилением зрения и возрастом. Exp. Physiol. 98, 546–555. DOI: 10.1113 / expphysiol.2012.067975
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Кеннеди, Д. М., и Кристу, Э. А. (2011). Большой объем визуальной информации усугубляет контроль силы у пожилых людей во время постоянных изометрических сокращений. Exp. Brain Res. 213, 351–361. DOI: 10.1007 / s00221-011-2777-x
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Кристева Р., Патино Л., и Омлор, В. (2007). Спектральная мощность кортикальной моторики в β-диапазоне и кортико-мышечная когерентность как механизм эффективного кортикоспинального взаимодействия во время установившегося моторного выхода. Neuroimage 36, 785–792. DOI: 10.1016 / j.neuroimage.2007.03.025
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Лэйдлоу, Д. Х., Корнац, К. В., Кин, Д. А., Сузуки, С., и Энока, Р. М. (1999). Силовые тренировки улучшают устойчивость сокращений медленного удлинения, выполняемых пожилыми людьми. J. Appl. Physiol. 87, 1786–1795.
PubMed Аннотация | Google Scholar
Лайне, К. М., Явуз, С. У., Фарина, Д. (2014). Связанные с задачей изменения в сенсомоторной интеграции влияют на общий синаптический вход для двигательных нейронов. Acta Physiol. 211, 229–239. DOI: 10.1111 / apha.12255
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Лодха, Н., Мун, Х., Ким, К., Онушко, Т., и Кристу, Э. А. (2016). Вариабельность моторной мощности ухудшает способность к вождению у пожилых людей. J. Gerontol. Биол. Sci. Med. Sci. 71, 1676–1681. DOI: 10.1093 / gerona / glw013
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Мартинес-Вальдес, Э., Лайне, К. М., Фалла, Д., Майер, Ф., и Фарина, Д. (2016). Поверхностная электромиография высокой плотности обеспечивает надежную оценку поведения двигательных единиц. Clin. Neurophysiol. 127, 2534–2541. DOI: 10.1016 / j.clinph.2015.10.065
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Макдоннелл, М.Д. и Эбботт Д. (2009). Что такое стохастический резонанс? Определения, заблуждения, дебаты и его отношение к биологии. PLoS Comput. Биол. 5: e1000348. DOI: 10.1371 / journal.pcbi.1000348
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Моррисон, С., Ньюэлл, К. М. (2015). Размерность и сложность движений и осанки человека. Нелинейная динамика Psychol. Life Sci. 19, 395–418.
PubMed Аннотация | Google Scholar
Мосс, Ф., Уорд, Л. М., и Саннита, В. Г. (2004). Стохастический резонанс и обработка сенсорной информации: учебное пособие и обзор приложения. Clin. Neurophysiol. 115, 267–281. DOI: 10.1016 / j.clinph.2003.09.014
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Nawab, S.H., Wotiz, R., and De Luca, C.J. (2004). «Разрешение наложения импульсов ЭМГ с помощью максимизации полезности», в Proceedings of the 8th World Multiconf Systemics Cybernetics, Informatics (Orlando, FL), 233–236.
Парк С. Х., Квон М. и Христу Э. А. (2017). Колебания выходной мощности двигателя с усилением визуальной обратной связи у пожилых людей. Neurosci. Lett. 647, 8–13. DOI: 10.1016 / j.neulet.2017.03.011
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Петик, Дж., Уинтер, С. Л., и Бернли, М. (2015). Усталость снижает сложность колебаний крутящего момента разгибателей колена во время максимальных и субмаксимальных прерывистых изометрических сокращений у человека. J. Physiol. 593, 2085–2096. DOI: 10.1113 / jphysiol.2015.284380
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Соснофф, Дж. Дж., И Ньюэлл, К. М. (2006). Ограничения обработки информации при старении при визуальном масштабировании изометрической силы. Exp. Brain Res. 170, 423–432. DOI: 10.1007 / s00221-005-0225-5
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Соснофф, Дж. Дж., И Ньюэлл, К. М. (2008). Возрастная потеря приспособляемости к быстрым временным шкалам двигательной изменчивости. J. Gerontol. B Psychol. Sci. Soc. Sci. 63, P344 – P352. DOI: 10.1093 / geronb / 63.6.p344
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Темпрадо, Дж. Дж., Виелуф, С., Слеймен-Малкун, Р. (2017). Возрастные изменения в управлении силами в разных контекстах задач. Exp. Brain Res. 235, 231–246. DOI: 10.1007 / s00221-016-4787-1
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Тоосизаде, Н., Молер, Дж., Вендель, К., и Наджафи, Б. (2015). Влияние синдрома слабости на разомкнутую и замкнутую стратегию постурального контроля. Геронтология 61, 51–60. DOI: 10.1159 / 000362549
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Трейси, Б. Л., Диненно, Д. В., Йоргенсен, Б., и Уэлш, С. Дж. (2007). Старение, зрительно-моторная коррекция и колебания силы в крупных мышцах. Med. Sci. Спортивные упражнения. 39, 469–479. DOI: 10.1249 / mss.0b013e31802d3ad3
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Трейси, Б.Л. и Энока Р. М. (2002). Пожилые люди менее устойчивы во время субмаксимальных изометрических сокращений мышц-разгибателей колена. J. Appl. Physiol. 92, 1004–1012. DOI: 10.1152 / japplphysiol.00954.2001
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Трейси, Б. Л., Хичкок, Л. Н., Уэлш, С. Дж., Пакстон, Р. Дж., И Фельдман-Кот, К. Э. (2015). Зрительно-моторная коррекция является важным фактором вариабельности силы при отведении указательного пальца пожилыми людьми. Фронт. Aging Neurosci. 7: 229. DOI: 10.3389 / fnagi.2015.00229
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Трейси, Б. Л., Малуф, К. С., Стефенсон, Дж. Л., Хантер, С. К., и Энока, Р. М. (2005). Вариабельность разряда двигательных единиц и колебания силы в диапазоне мышечных сил у пожилых людей. Мышечный нерв 32, 533–540. DOI: 10.1002 / mus.20392
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Vaillancourt, D.Э., Ларссон, Л., и Ньюэлл, К. М. (2002). Зависящая от времени структура скорости разряда двигательных единиц человека. Clin. Neurophysiol. 113, 1325–1338. DOI: 10.1016 / s1388-2457 (02) 00167-0
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Vaillancourt, D. E., and Newell, K. M. (2003). Старение и временная и частотная структура изменчивости силового воздействия. J. Appl. Physiol. 94, 903–912. DOI: 10.1152 / japplphysiol.00166.2002
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Ван Гервен, П.У. М., и Геррейро, М. Дж. С. (2016). Избирательное внимание и сенсорная модальность в старении: проклятия и благословения. Фронт. Гм. Neurosci. 10: 147. DOI: 10.3389 / fnhum.2016.00147
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Виелуф, С., Темпрадо, Дж. Дж., Бертон, Э., Джирса, В. К., и Слеймен-Малкун, Р. (2015). Влияние задачи и возраста на величину и структуру колебаний силы: понимание основных нейроповеденческих процессов. BMC Neurosci. 16:12. DOI: 10.1186 / s12868-015-0153-7
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Витте, М., Патино, Л., Андрикевич, А., Хепп-Реймонд, М. К., и Кристева, Р. (2007). Модуляция когерентности кортикально-мышечного β-диапазона человека с помощью статических сил низкого уровня. евро. J. Neurosci. 26, 3564–3570. DOI: 10.1111 / j.1460-9568.2007.05942.x
PubMed Аннотация | CrossRef Полный текст | Google Scholar
.
 Опишите этот процесс более подробно, в частности, объясните, как он связан с тем фактом, что кинетическое трение меньше статического. (Тот же процесс проскальзывания-захвата происходит, когда шины скрипят о тротуар.)
Опишите этот процесс более подробно, в частности, объясните, как он связан с тем фактом, что кинетическое трение меньше статического. (Тот же процесс проскальзывания-захвата происходит, когда шины скрипят о тротуар.) 0 кг ее массы на этом колене? (б) Во время интенсивных упражнений к суставам можно приложить усилия, которые легко в десять раз превышают поддерживаемый вес. Какова максимальная сила трения в таких условиях? Силы трения в суставах относительно малы при любых обстоятельствах, за исключением случаев, когда суставы ухудшаются, например, в результате травмы или артрита. Повышенные силы трения могут вызвать дальнейшие повреждения и боль.
0 кг ее массы на этом колене? (б) Во время интенсивных упражнений к суставам можно приложить усилия, которые легко в десять раз превышают поддерживаемый вес. Какова максимальная сила трения в таких условиях? Силы трения в суставах относительно малы при любых обстоятельствах, за исключением случаев, когда суставы ухудшаются, например, в результате травмы или артрита. Повышенные силы трения могут вызвать дальнейшие повреждения и боль.
 )
)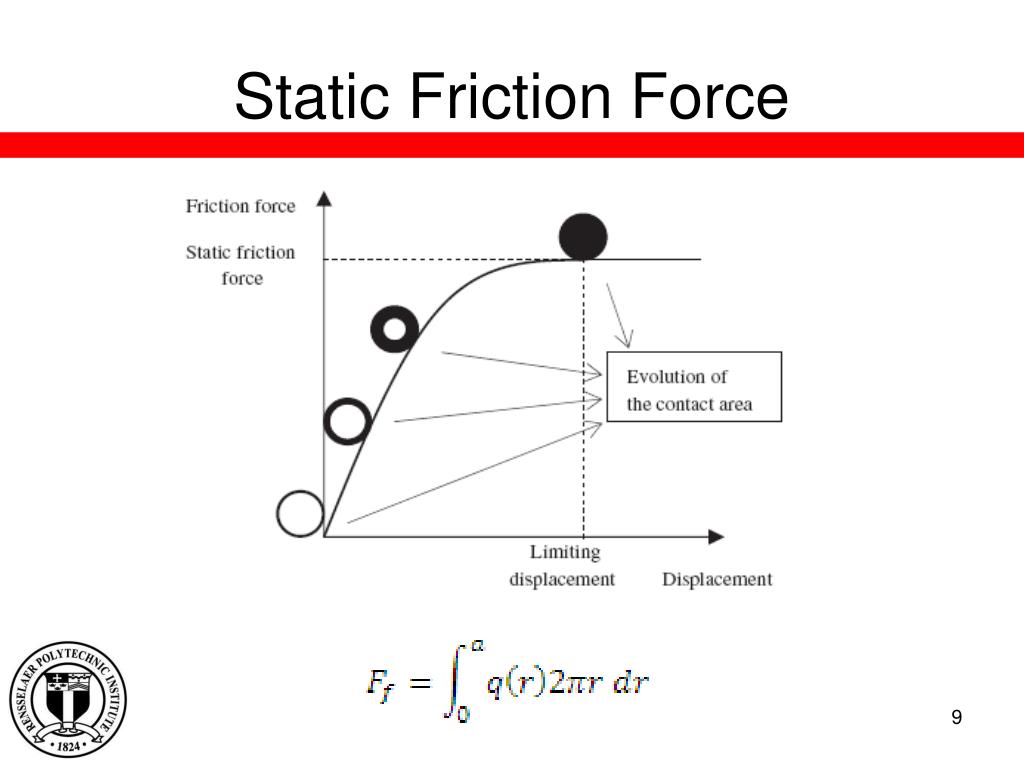 Ясно покажите, как вы следуете шагам, указанным в Стратегиях решения проблем.
Ясно покажите, как вы следуете шагам, указанным в Стратегиях решения проблем.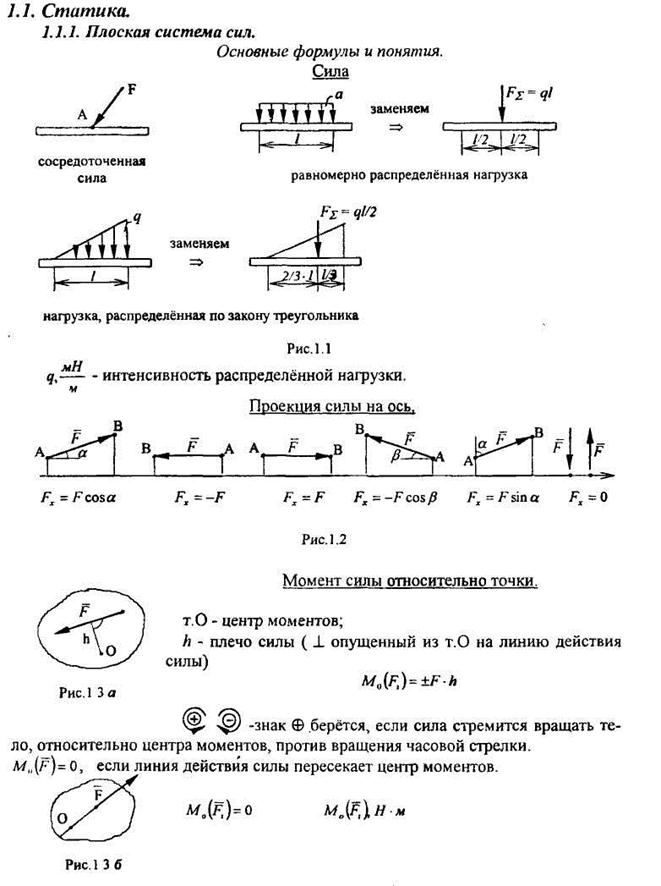 (Не обращайте внимания на прокатку.) Рассчитайте для автомобиля: (a) На сухом бетоне; б) на мокром бетоне; (c) На льду, при условии, что [latex] {\ mu} _ {\ text {s}} = 0,100 \\ [/ latex], то же самое, что и для обуви на льду.
(Не обращайте внимания на прокатку.) Рассчитайте для автомобиля: (a) На сухом бетоне; б) на мокром бетоне; (c) На льду, при условии, что [latex] {\ mu} _ {\ text {s}} = 0,100 \\ [/ latex], то же самое, что и для обуви на льду. Альпинист с весом 0 кг на рис. 7. (a) Найдите натяжение веревки и силу, которую альпинист должен приложить ногами к вертикальной поверхности скалы, чтобы оставаться в неподвижном состоянии. Предположим, что сила прилагается параллельно ее ногам. Также предположим, что ее руки оказывают незначительное усилие; б) Каков минимальный коэффициент трения между ее туфлями и обрывом?
Альпинист с весом 0 кг на рис. 7. (a) Найдите натяжение веревки и силу, которую альпинист должен приложить ногами к вертикальной поверхности скалы, чтобы оставаться в неподвижном состоянии. Предположим, что сила прилагается параллельно ее ногам. Также предположим, что ее руки оказывают незначительное усилие; б) Каков минимальный коэффициент трения между ее туфлями и обрывом?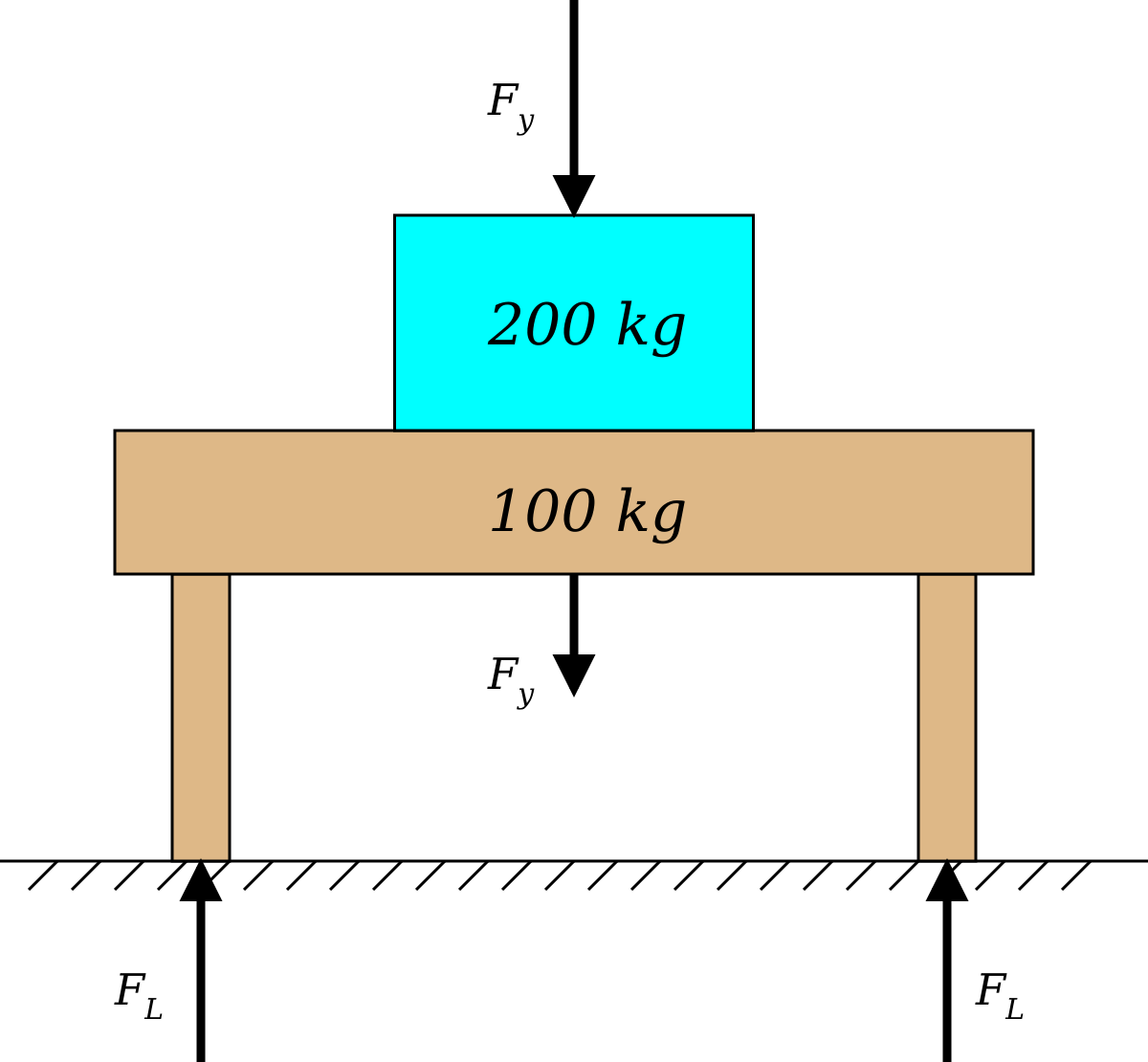

 Р.П. Фейнман, Р.П. Лейтон и М. Сэндс, Лекции Фейнмана по физике, том I, стр. 12-5, Addison-Wesley, 1964.
Р.П. Фейнман, Р.П. Лейтон и М. Сэндс, Лекции Фейнмана по физике, том I, стр. 12-5, Addison-Wesley, 1964. 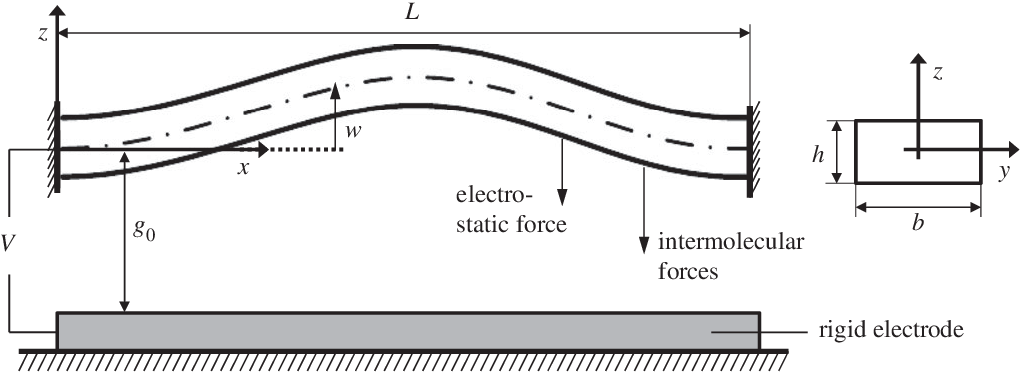 74
74